Узловые точки на криволинейных участках профиля детали
Профиль детали, обрабатываемой фасонным резцом, состоит из сопряженных прямолинейных и криволинейных участков нескольких типов (см. рис.4.1, 4.2):
1) прямолинейных участков, параллельных оси детали (T3?T4, T5?T6);
2) прямолинейных радиальных участков (T7?T9);
3) прямолинейных участков, расположенных под углом к оси изделия и соответствующих коническим участкам обрабатываемой детали (T2?T3);
4) криволинейных участков (T4?T5), чаще всего очерченных по дуге окружности.
Каждому из прямолинейных участков профиля детали соответствует прямолинейный участок профиля инструмента (в том числе и участкам, соответствующим коническим элементам изделия). Аналогично, каждому криволинейному участку профиля детали соответствует криволинейный участок режущей кромки фасонного инструмента.
Любая прямая на плоскости описывается линейным уравнением, содержащим два независимых параметра [4, С.60]:


где b=C/B и k=-A/C. Тогда для однозначного описания прямой на плоскости достаточно задать две точки, через которые проходит данная прямая, что приведет к следующей записи уравнения прямой:

где T1(x1, y1) и T2(x2, y2) - две точки, через которые проходит заданная прямая.
Большинство кривых линий на плоскости (в том числе все кривые второго порядка - окружность, эллипс, парабола, гипербола) описываются функциями, имеющими более чем два независимых параметра. Так, для однозначного задания окружности требуется определение трех параметров, а для задания произвольного эллипса - пяти параметров (например, координат фокусов эллипса и величины большой полуоси).
Проведенные рассуждения позволяют сделать важный вывод: для однозначного описания криволинейного участка профиля детали недостаточно задания координат граничных точек. Помимо граничных точек, должны быть заданы одна или несколько промежуточных точек участка.
Количество необходимых промежуточных точек определяется типом линии, по которой очерчен криволинейный участок. Таким образом, для однозначного задания кривой линии на плоскости, как правило, требуется определение более чем двух параметров, и, следовательно, задание более чем двух узловых точек.
Наиболее часто кривые, по которым очерчиваются криволинейные элементы профиля детали, представляют собой дуги окружностей. Для однозначного определения окружности требуется задание трех узловых точек. Так как две из трех узловых точек являются граничными точками криволинейного участка профиля детали, их координаты могут быть определены непосредственно из чертежа. Таким образом, при подготовке исходных данных для коррекционного расчета профиля стоит задача определения координат одной промежуточной точки для каждого из криволинейных участков, очерченных по дуге окружности.
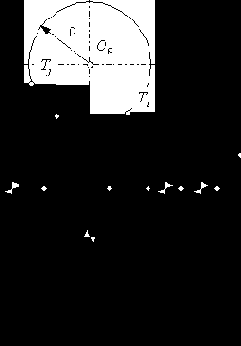
Как правило, на чертеже детали участок, очерченный по дуге окружности, задается координатами центра окружности и ее радиусом (см. рис. 4.1). Таким образом, на этапе выделения узловых точек необходимо решить задачу определения координат промежуточной точки по координатам центра окружности и ее радиусу. Решение этой задачи сводится к решению единственного квадратного уравнения (уравнения окружности):

где x, y - координаты точки окружности в системе координат XY, xr, yr - координаты центра окружности в системе XY, r - радиус окружности (см. рис. 4.4).
 Рис. 4.4. Схема к определению уравнения окружности |
На рис. 4. 5 представлены схемы, иллюстрирующие проведение расчетов координат промежуточной узловой точки применением координатных систем, определенных на чертеже детали. Последовательность вычислений, необходимых для определения координат промежуточной узловой точки криволинейного участка может быть сформулирована в виде следующего алгоритма:
1. Определить радиус окружности r и координаты lr, rr ее центра (точки Or) в системе координат, связанной с деталью.
2. Назначить координату lk или координату rk искомой узловой точки. Выбор назначаемой координаты не имеет принципиального значения. Однако в практике рекомендуется назначать координату по следующему правилу: если выполняется условие

то назначается координата lk, в противном случае назначается координата rk. Следует стремиться к тому, чтобы точка Tk располагалась вблизи середины участка Ti?Tj. Для этого ее назначаемую координату (соответственно, lk или rk) рассчитывают по одной из формул:


Для удобства последующих вычислений значение, полученное по формуле, округляется до целого числа.
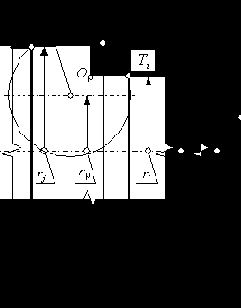
а б
Рис. 4.5. Схема к определению координат промежуточной узловой точки на участке, образованном дугой окружности
3. В уравнение окружности

подставляются координаты центра окружности lr и rr, значение радиуса окружности r и значение одной из координат точки Tk (lk или rk). Полученное уравнение решается относительно второй координаты узловой точки (соответственно, rk или lk).
4. На основе анализа чертежа детали из полученных корней уравнения выделяется корень, определяющий искомую координату точки Tk. Расчет ведется с точностью до 0,001.
