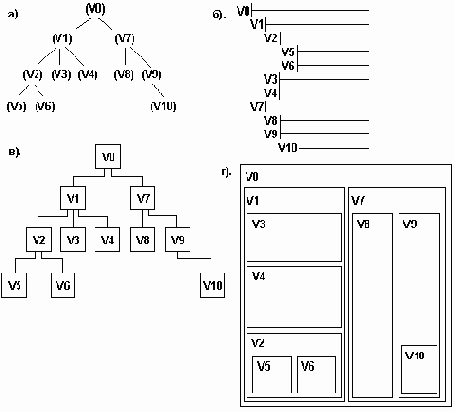
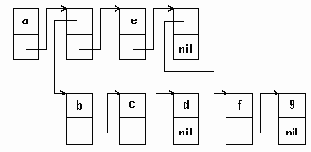
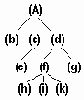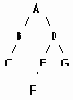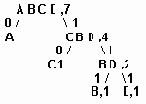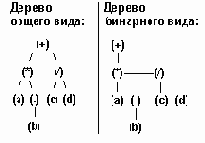Дерево
рис. 6.8. Дерево
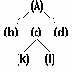
Лес
рис. 6.9. Лес
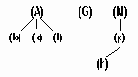
Ниже будет представлен важный класс орграфов - ориентированные деревья - и соответствующая им терминология. Деревья нужны для описания любой структуры с иерархией. Традиционные примеры таких структур: генеалогические деревья, десятичная классификация книг в библиотеках, иерархия должностей в организации, алгебраическое выражение, включающее операции, для которых предписаны определенные правила приоритета.
Ориентированное дерево - это такой ациклический орграф (ориентированный граф), у которого одна вершина, называемая корнем, имеет полустепень захода, равную 0, а остальные - полустепени захода, равные 1. Ориентированное дерево должно иметь по крайней мере одну вершину. Изолированная вершина также представляет собой ориентированное дерево.
Вершина ориентированного дерева, полустепень исхода которой равна нулю, называется КОНЦЕВОЙ (ВИСЯЧЕЙ) вершиной или ЛИСТОМ; все остальные вершины дерева называют вершинами ветвления. Длина пути от корня до некоторой вершины называется УРОВНЕМ (НОМЕРОМ ЯРУСА) этой вершины. Уровень корня ориентированного дерева равен нулю, а уровень любой другой вершины равен расстоянию (т.е. модулю разности номеров уровней вершин) между этой вершиной и корнем. Ориентированное дерево является ациклическим графом, все пути в нем элементарны.
Во многих приложениях относительный порядок следования вершин на каждом отдельном ярусе имеет определенное значение. При представлении дерева в ЭВМ такой порядок вводится автоматически, даже если он сам по себе произволен. Порядок следования вершин на некотором ярусе можно легко ввести, помечая одну вершину как первую, другую - как вторую и т.д. Вместо упорядочивания вершин можно задавать порядок на ребрах. Если в ориентированном дереве на каждом ярусе задан порядок следования вершин, то такое дерево называется УПОРЯДОЧЕННЫМ ДЕРЕВОМ.
Введем еще некоторые понятия, связанные с деревьями. На рис.6.10 показано дерево:
Узел X называется ПРЕДКОМ (или ОТЦОМ), а узлы Y и Z называются НАСЛЕДНИКАМИ (или СЫНОВЬЯМИ) их соответственно между собой называют БРАТЬЯМИ. Причем левый сын является старшим сыном, а правый - младшим. Число поддеревьев данной вершины называется СТЕПЕНЬЮ этой вершины. ( В данном примере X имеет 2 поддерева, следовательно СТЕПЕНЬ вершины X равна 2).
Дерево
рис.6.10. Дерево
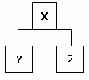
Если из дерева убрать корень и ребра, соединяющие корень с вершинами первого яруса, то получится некоторое множество несвязанных деревьев. Множество несвязанных деревьев называется ЛЕСОМ (рис. 6.9).
Упорядоченный лес
рис.6.17. Упорядоченный лес
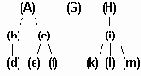
Машинное представление десятичных чисел в упакованном формате
Рисунок2.6. Машинное представление десятичных чисел в упакованном формате
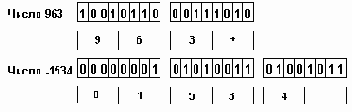
Каждая десятичная цифра числа занимает полбайта (4 двоичных разряда) и представляется в этом полубайте ее двоичным кодом. Еще полбайта занимает знак числа, который представляется двоичным кодом 1010 - знак "+" или 1011 - знак "-". Представление занимает целое число байт и при необходимости дополняется ведущим нулем.
Машинное представление десятичных чисел в зонном формате
Рисунок2.7. Машинное представление десятичных чисел в зонном формате
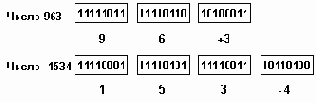
Внутримашинное представление этого типа, так называемый десятичный зонный формат, весьма близок к такому представлению данных, которое удобно пользователю: каждая десятичная цифра представляется байтом: содержащим код символа соответствующей цифры. В IBM System/390, которая аппаратно поддерживает зонный формат, применяется символьный код EBCDIC, в котором код символа цифры содержит в старшем полубайте код 1111, а в младшем - двоичный код цифры числа. Знак не входит в общее число цифр в числе, для представления знака в старшем полубайте последней цифры числа код 1111 заменяется на 1010 - знак "+" или 1011 - знак "-".
Примеры представления чисел в зонном формате приведены на рис.2.7.
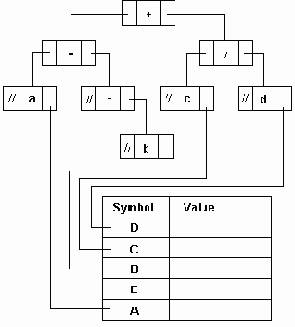
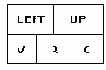
На рис. 3.7 приведена многосвязная структура, в которой используются вершины такого типа для представления матрицы А, описанной ранее в данном пункте. Циклический список представляет все строки и столбцы. Список столбца может содержать общие вершины с одним списком строки или более. Для того, чтобы обеспечить использование более эффективных алгоритмов включения и исключения элементов, все списки строк и столбцов имеют головные вершины. Головная вершина каждого списка строки содержит нуль в поле С; аналогично каждая головная вершина в списке столбца имеет нуль в поле R. Строка или столбец, содержащие только нулевые элементы, представлены головными вершинами, у которых поле LEFT или UP указывает само на себя.
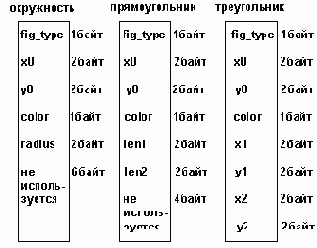
Как видно из рисунка, под запись с вариантами выделяется в любом случае объем памяти, достаточный для размещения самого большого варианта. Если же выделенная память используется для меньшего варианта, часть ее остается неиспользуемой. Общая для всех вариантов часть записи размещается так, чтобы смещения всех полей относительно начала записи были одинаковыми для всех вари- антов. Очевидно, что наиболее просто это достигается размещением общих полей в начале записи, но это не строго обязательно. Вариантная часть может и "вклиниваться" между полями общей части. Поскольку в любом случае вариантная часть имеет фиксированный (максимальный) размер, смещения полей общей части также останутся фиксированными.
Пирамида турнирной сортировки
Рисунок3.13. Пирамида турнирной сортировки
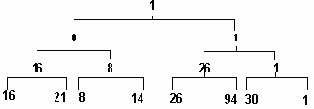
В примере 3.12 приведена программная иллюстрация алгоритма турнирной сортировки. Она нуждается в некоторых пояснениях. Построение пирамиды выполняется функцией Create_Heap. Пирамида строится от основания к вершине. Элементы, составляющие каждый уровень, связываются в линейный список, поэтому каждый узел дерева помимо обычных указателей на потомков - left и right - содержит и указатель на "брата" - next. При работе с каждым уровнем указатель содержит начальный адрес списка элементов в данном уровне. В первой фазе строится линейный список для нижнего уровня пирамиды, в элементы которого заносятся ключи из исходной последовательности. Следующий цикл while в каждой своей итерации надстраивает следующий уровень пирамиды. Условием завершения этого цикла является получение списка, состоящего из единственного элемента, то есть, вершины пирамиды. Построение очередного уровня состоит в попарном переборе элементов списка, составляющего предыдущий (нижний) уровень. В новый уровень переносится наименьшее значение ключа из каждой пары.
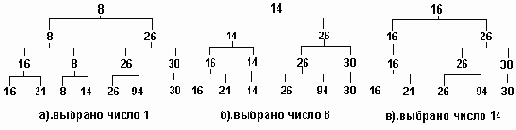
Следующий этап состоит в выборке значений из пирамиды и формирования из них упорядоченной последовательности (процедура Heap_Sort и функция Competit). В каждой итерации цикла процедуры Heap_Sort выбирается значение из вершины пирамиды - это наименьшее из имеющихся в пирамиде значений ключа. Узел-вершина при этом освобождается, освобождаются также и все узлы, занимаемые выбранным значением на более низких уровнях пирамиды. За освободившиеся узлы устраивается (снизу вверх) состязание между их потомками. Так, для пирамиды, исходное состояние которой было показано на рис 3. , при выборке первых трех ключей (1, 8, 14) пирамида будет последовательно принимать вид, показанный на рис.3.14 (символом x помечены пустые места в пирамиде).
Пирамида после последовательных выборок
Рисунок3.14. Пирамида после последовательных выборок
Процедура Heap_Sort получает входной параметр ph - указатель на вершину пирамиды. и формирует выходной параметр a - упорядоченный массив чисел. Вся процедура Heap_Sort состоит из цикла, в каждой итерации которого значение из вершины переносится в массив a, а затем вызывается функция Competit, которая обеспечивает реорганизацию пирамиды в связи с удалением значения из вершины.
Функция Competet рекурсивная, ее параметром является указатель на вершину того поддерева, которое подлежит реорганизации. В первой фазе функции устанавливается, есть ли у узла, составляющего вершину заданного поддерева, потомок, значение данных в котором совпадает со значением данных в вершине. Если такой потомок есть, то функция Competit вызывает сама себя для реорганизации того поддерева, вершиной которого является обнаруженный потомок. После реорганизации адрес потомка в узле заменяется тем адресом, который вернул рекурсивный вызов Competit. Если после реорганизации оказывается, что у узла нет потомков (или он не имел потомков с самого начала), то узел уничтожается и функция возвращает пустой указатель. Если же у узла еще остаются потомки, то в поле данных узла заносится значение данных из того потомка, в котором это значение наименьшее, и функция возвращает прежний адрес узла.
{===== Программный пример 3.12 =====} { Турнирная сортировка } type nptr = ^node; { указатель на узел } node = record { узел дерева } key : integer; { данные } left, right : nptr; { указатели на потомков } next : nptr; { указатель на "брата" } end; { Создание дерева - функция возвращает указатель на вершину созданного дерева } Function Heap_Create(a : Seq) : nptr; var i : integer; ph2 : nptr; { адрес начала списка уровня } p1 : nptr; { адрес нового элемента } p2 : nptr; { адрес предыдущего элемента } pp1, pp2 : nptr; { адреса соревнующейся пары } begin { Фаза 1 - построение самого нижнего уровня пирамиды } ph2:=nil; for i:=1 to n do begin New(p1); { выделение памяти для нового эл-та } p1^.key:=a[i]; { запись данных из массива } p1^.left:=nil; p1^.right:=nil; { потомков нет } { связывание в линейный список по уровню } if ph2=nil then ph2:=p1 else p2^.next:=p1; p2:=p1; end; { for } p1^.next:=nil; { Фаза 2 - построение других уровней } while ph2^.next<>nil do begin { цикл до вершины пирамиды } pp1:=ph2; ph2:=nil; { начало нового уровня } while pp1<>nil do begin { цикл по очередному уровню } pp2:=pp1^.next; New(p1); { адреса потомков из предыдущего уровня } p1^.left:=pp1; p1^.right:=pp2; p1^.next:=nil; { связывание в линейный список по уровню } if ph2=nil then ph2:=p1 else p2^.next:=p1; p2:=p1; { состязание данных за выход на уровень } if (pp2=nil)or(pp2^.key > pp1^.key) then p1^.key:=pp1^.key else p1^.key:=pp2^.key; { переход к следующей паре } if pp2<>nil then pp1:=pp2^.next else pp1:=nil; end; { while pp1<>nil } end; { while ph2^.next<>nil } Heap_Create:=ph2; end; { Реорганизация поддерева - функция возвращает указатель на вершину реорганизованного дерева } Function Competit(ph : nptr) : nptr; begin { определение наличия потомков, выбор потомка для реорганизации, реорганизация его } if (ph^.left<>nil)and(ph^.left^.key=ph^.key) then ph^.left:=Competit(ph^.left) else if (ph^.right<>nil) then ph^.right:=Competit(ph^.right); if (ph^.left=nil)and(ph^.right=nil) then begin { освобождение пустого узла } Dispose(ph); ph:=nil; end; else { состязание данных потомков } if (ph^.left=nil) or ((ph^.right<>nil)and(ph^.left^.key > ph^.right^.key)) then ph^.key:=ph^.right^.key else ph^.key:=ph^.left^.key; Competit:=ph; end; { Сортировка } Procedure Heap_Sort(var a : Seq); var ph : nptr; { адрес вершины дерева } i : integer; begin ph:=Heap_Create(a); { создание дерева } { выборка из дерева } for i:=1 to N do begin { перенос данных из вершины в массив } a[i]:=ph^.key; { реорганизация дерева } ph:=Competit(ph); end; end;
Построение дерева требует N-1 сравнений, выборка - N*log2(N) сравнений. Порядок алгоритма, таким образом, O(N*log2(N)). Сложность операций над связными структурами данных, однако, значительно выше, чем над статическими структурами. Кроме того, алгоритм неэкономичен в отношении памяти: дублирование данных на разных уровнях пирамиды приводит к тому, что рабочая область памяти содержит примерно 2*N узлов.
Частично упорядоченное дерево
Рисунок3.15. Частично упорядоченное дерево
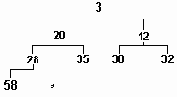
Представление дерева в виде пирамиды наглядно показывает нам, что для такого дерева можно ввести понятия "начала" и "конца". Началом, естественно, будет считаться вершина пирамиды, а концом - крайний левый элемент в самом нижнем ряду (на рис.3.15 это 58).
Для сортировки этим методом должны быть определены две операции: вставка в дерево нового элемента и выборка из дерева минимального элемента; причем выполнение любой из этих операций не должно нарушать ни сформулированной выше частичной упорядоченности дерева, ни его сбалансированности.
Алгоритм вставки состоит в следующем. Новый элемент вставляется на первое свободное место за концом дерева (на рис.3.15 это место обозначено символом "*"). Если ключ вставленного элемента меньше, чем ключ его предка, то предок и вставленный элемент меняются местами. Ключ вставленного элемента теперь сравнивается с ключом его предка на новом месте и т.д. Сравнения заканчиваются, когда ключ нового элемента окажется больше ключа предка или когда новый элемент "выплывет" в вершину пирамиды. Пирамида, показанная на рис.3.15, построена именно последовательным включением в нее чисел из приведенного ряда. Если мы включим в нее, например, еще число 16, то пирамида примет вид, представленный на рис.3.16. (Символом "*" помечены элементы, перемещенные при этой операции.)
Частично упорядоченное дерево, включение элемента
Рисунок3.16. Частично упорядоченное дерево, включение элемента
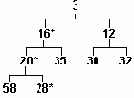
Процедура выборки элемента несколько сложнее. Очевидно, что минимальный элемент находится в вершине. После выборки за освободившееся место устраивается состязание между потомками, и в вершину перемещается потомок с наименьшим значением ключа. За освободившееся место перемешенного потомка состязаются его потомки и т.д., пока свободное место не опустится до листа пирамиды. Состояние нашего дерева после выборки из него минимального числа (3) показано на рис.3.17.а.
Частично упорядоченное дерево, исключение элемента
Рисунок3.17. Частично упорядоченное дерево, исключение элемента
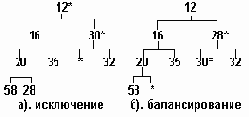
Упорядоченность дерева восстановлена, но нарушено условие его сбалансированности, так как свободное место находится не в конце дерева. Для восстановления сбалансированности последний элемент дерева переносится на освободившееся место, а затем "всплывает" по тому же алгоритму, который применялся при вставке. Результат такой балансировки показан на рис.3.17.б.
Прежде, чем описывать программный пример, иллюстрирующий сортировку частично упорядоченным деревом - пример 3.13, обратим внимание читателей на способ, которым в нем дерево представлено в памяти. Это способ представления двоичных деревьев в статической памяти (в одномерном массиве), который может быть применен и в других задачах. Элементы дерева располагаются в соседних слотах памяти по уровням. Самый первый слот выделенной памяти занимает вершина. Следующие 2 слота - элементы второго уровня, следующие 4 слота - третьего и т.д. Дерево с рис.3.17.б, например, будет линеаризовано таким образом:
12 16 28 20 35 30 32 58
В таком представлении отпадает необходимость хранить в составе узла дерева указатели, так как адреса потомков могут быть вычислены. Для узла, представленного элементом массива с индексом i индексы его левого и правого потомков будут 2*i и 2*i+1 соответственно. Для узла с индексом i индекс его предка будет i div 2.
После всего вышесказанного алгоритм программного примера 3.13 не нуждается в особых пояснениях. Поясним только структуру примера. Пример оформлен в виде законченного программного модуля, который будет использован и в следующем примере. Само дерево представлено в массиве tree, переменная nt является индексом первого свободного элемента в массиве. Входные точки модуля:
процедура InitST - инициализация модуля, установка начального значения nt; функция InsertST - вставка в дерево нового элемента; функция возвращает false, если в дереве нет свободного места, иначе - true; функция DeleteST - выборка из дерева минимального элемента; функция возвращает false, если дерево пустое, иначе - true; функция CheckST - проверка состояния дерева: ключ минимального элемента возвращается в выходном параметре, но элемент не исключается из дерева; а возвращаемое значение функции - 0 - если дерево пустое, 1 - если дерево заполнено не до конца, 2 - если дерево заполнено до конца.
Кроме того в модуле определены внутренние программные единицы:
функция Down - обеспечивает спуск свободного места из вершины пирамиды в ее основание, функция возвращает индекс свободного места после спуска; процедура Up - обеспечивающая всплытие элемента с заданного места.
{===== Программный пример 3.13 =====} { Сортировка частично упорядоченным деревом } Unit SortTree; Interface Procedure InitSt; Function CheckST(var a : integer) : integer; Function DeleteST(var a : integer) : boolean; Function InsertST(a : integer) : boolean; Implementation Const NN=16; var tr : array[1..NN] of integer; { дерево } nt : integer; { индекс последнего эл-та в дереве } {** Всплытие эл-та с места с индексом l **} Procedure Up(l : integer); var h : integer; { l - индекс узла, h - индекс его предка } x : integer; begin h:=l div 2; { индекс предка } while h > 0 do { до начала дерева } if tr[l] < tr[h] then begin { ключ узла меньше, чем у предка } x:=tr[l]; tr[l]:=tr[h]; tr[h]:=x; { перестановка } l:=h; h:=l div 2; { предок становится текущим узлом } end else h:=0; { конец всплытия } end; { Procedure Up } {** Спуск свободного места из начала дерева **} Function Down : integer; var h, l : integer; { h - индекс узла, l - индекс его потомка } begin h:=1; { начальный узел - начало дерева } while true do begin l:=h*2; { вычисление индекса 1-го потомка } if l+1
Если применять сортировку частично упорядоченным деревом для упорядочения уже готовой последовательности размером N, то необходимо N раз выполнить вставку, а затем N раз - выборку. Порядок алгоритма - O(N*log2(N)), но среднее значение количества сравнений примерно в 3 раза больше, чем для турнирной сортировки. Но сортировка частично упорядоченным деревом имеет одно существенное преимущество перед всеми другими алгоритмами. Дело в том, что это самый удобный алгоритм для "сортировки on-line", когда сортируемая последовательность не зафиксирована до начала сортировки, а меняется в процессе работы и вставки чередуются с выборками. Каждое изменение (добавление/удаление элемента) сортируемой последовательности потребует здесь не более, чем 2*log2(N) сравнений и перестановок, в то время, как другие алгоритмы потребуют при единичном изменении переупорядочивания всей последовательности "по полной программе".
Типичная задача, которая требует такой сортировки, возникает при сортировке данных на внешней памяти (файлов). Первым этапом такой сортировки является формирование из данных файла упорядоченных последовательностей максимально возможной длины при ограниченном объеме оперативной памяти. Приведенный ниже программный пример (пример 3.14) показывает решение этой задачи.
Последовательность чисел, записанная во входном файле поэлементно считывается и числа по мере считывания включаются в дерево. Когда дерево оказывается заполненным, очередное считанное из файла число сравнивается с последним числом, выведенным в выходной файл. Если считанное число не меньше последнего выведенного, но меньше числа, находящегося в вершине дерева, то в выходной файл выводится считанное число. Если считанное число не меньше последнего выведенного, и не меньше числа, находящегося в вершине дерева, то в выходной файл выводится число, выбираемое из дерево, а считанное число заносится в дерево. Наконец, если считанное число меньше последнего выведенного, то поэлементно выбирается и выводится все содержимое дерева, и формирование новой последовательности начинается с записи в пустое дерево считанного числа.
{===== Программный пример 3.14 =====} { Формирование отсортированных последовательностей в файле } Uses SortTree; var x : integar; { считанное число } y : integer; { число в вершине дерева } old : integer; { последнее выведенное число } inp : text; { входной файл } out : text; { выходной файл } bf : boolean; { признак начала вывода последовательности } bx : boolean; { рабочая переменная } begin Assign(inp,'STX.INP'); Reset(inp); Assign(out,'STX.OUT'); Rewrite(out); InitST; { инициализация сортировки } bf:=false; { вывод последовательности еще не начат } while not Eof(inp) do begin ReadLn(inp,x); { считывание числа из файла } { если в дереве есть свободное место - включить в дерево } if CheckST(y)
Представление строк переменной длины со счетчиком
Рисунок4.5. Представление строк переменной длины со счетчиком

В двух предыдущих вариантах обеспечивалось максимально эффективное расходование памяти (1-2 "лишних" символа на строку), но изменчивость строки обеспечивалась крайне неэффективно. Поскольку вектор - статическая структура, каждое изменение длины строки требует создания нового вектора, пересылки в него неизменяемой части строки и уничтожения старого вектора. Это сводит на нет все преимущества работы со статической памятью. Поэтому наиболее популярным способом представления строк в памяти являются вектора с управляемой длиной.
Представление строк вектором с управляемой длиной
Рисунок4.6. Представление строк вектором с управляемой длиной

В программном примере 4.4 приведен модуль, реализующий представление строк вектором с управляемой длиной и некоторые операции над такими строками. Для уменьшения объема в примере в секции Implementation определены не все процедуры/функции. Предоставляем читателю самостоятельно разработать прочие объявленные в секции Interface подпрограммы. Дескриптор строки описывается типом _strdescr, который в точности повторяет структуру, показанную на рис.4.6. Функция NewStr выделяет две области памяти: для дескриптора строки и для области данных строки. Адрес дескриптора строки, возвращаемый функцией NewStr - тип varstr - является той переменной, значение которой указывается пользователем модуля для идентификации конкретной строки при всех последующих операциях с нею. Область данных, указатель на которую заносится в дескрипторе строки - тип _dat_area - описана как массив символов максимального возможного объема - 64 Кбайт. Однако, объем памяти, выделяемый под область данных функцией NewStr, как правило, меньший - он задается параметром функции. Хотя индексы в массиве символов строки теоретически могут изменяться от 1 до 65535, значение индекса в каждой конкретной строке при ее обработке ограничивается полем maxlen дескриптора данной строки. Все процедуры/функции обработки строк работают с символами строки как с элементами вектора, обращаясь к ним по индексу. Адрес вектора процедуры получают из дескриптора строки. Обратите внимание на то, что в процедуре CopyStr длина результата ограничивается максимальной длиной целевой строки.
{==== Программный пример 4.4 ====} { Представление строк вектором с управляемой длиной } Unit Vstr; Interface type _dat_area = array[1..65535] of char; type _strdescr = record { дескриптор строки } maxlen, curlen : word; { максимальная и текущая длины } strdata : ^_dat_area; { указатель на данные строки } end; type varstr = ^_strdescr; { тип - СТРОКА ПЕРЕМЕННОЙ ДЛИНЫ } Function NewStr(len : word) : varstr; Procedure DispStr(s : varstr); Function LenStr(s : varstr) : word; Procedure CopyStr(s1, s2 : varstr); Function CompStr(s1, s2 : varstr) : integer; Function PosStr(s1, s2 : varstr) : word; Procedure ConcatStr(var s1: varstr; s2 : varstr); Procedure SubStr(var s1 : varstr; n, l : word); Implementation {** Создание строки; len - максимальная длина строки; ф-ция возвращает указатель на дескриптор строки } Function NewStr(len : word) : varstr; var addr : varstr; daddr : pointer; begin New(addr); { выделение памяти для дескриптора } Getmem(daddr,len); { выделение памяти для данных } { занесение в дескриптор начальных значений } addr^.strdata:=daddr; addr^.maxlen:=len; addr^.curlen:=0; Newstr:=addr; end; { Function NewStr } Procedure DispStr(s : varstr); {** Уничтожение строки } begin FreeMem(s^.strdata,s^.maxlen); { уничтожение данных } Dispose(s); { уничтожение дескриптора } end; { Procedure DispStr } {** Определение длины строки, длина выбирается из дескриптора } Function LenStr(s : varstr) : word; begin LenStr:=s^.curlen; end; { Function LenStr } Procedure CopyStr(s1, s2 : varstr); { Присваивание строк s1:=s2} var i, len : word; begin { длина строки-результата м.б. ограничена ее макс. длиной } if s1^.maxlen s2; -1 - если s1 < s2 } Function CompStr(s1, s2 : varstr) : integer; var i : integer; begin i:=1; { индекс текущего символа } { цикл, пока не будет достигнут конец одной из строк } while (i s2^.strdata^[i] then begin CompStr:=1; Exit; end; if s1^.strdata^[i] < s2^.strdata^[i] then begin CompStr:=-1; Exit; end; i:=i+1; { переход к следующему символу } end;
{ если выполнение дошло до этой точки, то найден конец одной из строк, и все сравненные до сих пор символы были равны; строка меньшей длины считается меньшей }
if s1^.curlens2^.curlen then CompStr:=1 else CompStr:=0; end; { Function CompStr } . . END.
Представление строки однонаправленным связным списком
Рисунок4.7. Представление строки однонаправленным связным списком

Представление строки двунаправленным связным списком
Рисунок4.8. Представление строки двунаправленным связным списком

Представление строки многосимвольными звеньями переменной длины
Рисунок4.10. Представление строки многосимвольными звеньями переменной длины
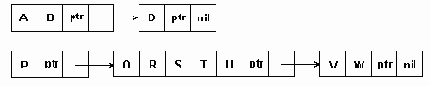
Такой метод спискового представления строк особенно удобен в задачах редактирования текста, когда большая часть операций приходится на изменение, вставку и удаление целых слов. Поэтому в этих задачах целесообразно список организовать так, чтобы каждый его элемент содержал одно слово текста. Символы пробела между словами в памяти могут не представляются.
Представление строки звеньями управляемой длины
Рисунок4.11. Представление строки звеньями управляемой длины
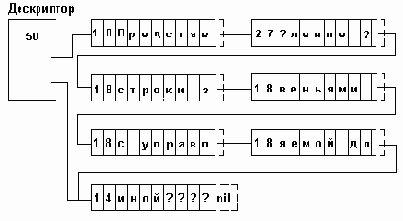
В программном примере 4.5 приведен модуль, реализующий представление строк звеньями с управляемой длиной. Даже с первого взгляда видно, что он значительно сложнее, чем пример 4.4. Это объясняется тем, что здесь вынуждены обрабатывать как связные (списки блоков), так и векторные (массив символов в каждом блоке) структуры. Поэтому при последовательной обработке символов строки процедура должна сохранять как адрес текущего блока, так и номер текущего символа в блоке. Для этих целей во всех процедурах/функциях используются переменные cp и bi соответственно. (Процедуры и функции, обрабатывающие две строки - cp1, bi1, cp2, bi2.) Дескриптор строки - тип _strdescr - и блок - тип _block - в точности повторяют структуру, показанную на рис.4.10. Функция NewStr выделяет память только для дескриптора строки и возвращает адрес дескриптора - тип varstr - он служит идентификатором строки при последующих операциях с нею. Память для хранения данных строки выделяется только по мере необходимости. Во всех процедурах/функциях приняты такие правила работы с памятью:
если выходной строке уже выделены блоки, используются эти уже выделенные блоки; если блоки, выделенные выходной строке исчерпаны, выделяются новые блоки - по мере необходимости; если результирующее значение выходной строки не использует все выделенные строке блоки, лишние блоки освобождаются.
Для освобождения блоков определена специальная внутренняя функция FreeBlock, освобождающая весь список блоков, голова которого задается ее параметром.
Обратите внимание на то, что ни в каких процедурах не контролируется максимальный объем строки результата - он может быть сколь угодно большим, а поле длины в дескрипторе строки имеет тип longint.
{==== Программный пример 4.5 ====} { Представление строки звеньями управляемой длины } Unit Vstr; Interface const BLKSIZE = 8; { число символов в блоке } type _bptr = ^_block; { указатель на блок } _block = record { блок } i1, i2 : byte; { номера 1-го и последнего символов } strdata : array [1..BLKSIZE] of char; { символы } next : _bptr; { указатель на следующий блок } end; type _strdescr = record { дескриптор строки } len : longint; { длина строки } first, last : _bptr; { указ.на 1-й и последний блоки } end; type varstr = ^_strdescr; { тип - СТРОКА ПЕРЕМЕННОЙ ДЛИНЫ } Function NewStr : varstr; Procedure DispStr(s : varstr); Function LenStr(s : varstr) : longint; Procedure CopyStr(s1, s2 : varstr); Function CompStr(s1, s2 : varstr) : integer; Function PosStr(s1, s2 : varstr) : word; Procedure ConcatStr(var s1: varstr; s2 : varstr); Procedure SubStr(var s : varstr; n, l : word); Implementation Function NewBlock :_bptr; {Внутр.функция-выделение нового блока} var n : _bptr; i : integer; begin New(n); { выделение памяти } n^.next:=nil; n^.i1:=0; n^.i2:=0; { начальные значения } NewBlock:=n; end; { NewBlock } {*** Внутр.функция - освобождение цепочки блока, начиная с c } Function FreeBlock(c : _bptr) : _bptr; var x : _bptr; begin { движение по цепочке с освобождением памяти } while c<>nil do begin x:=c; c:=c^.next; Dispose(x); end; FreeBlock:=nil; { всегда возвращает nil } end; { FreeBlock } Function NewStr : varstr; {** Создание строки } var addr : varstr; begin New(addr); { выделение памяти для дескриптора } { занесение в дескриптор начальных значений } addr^.len:=0; addr^.first:=nil; addr^.last:=nil; Newstr:=addr; end; { Function NewStr } Procedure DispStr(s : varstr); {** Уничтожение строки } begin s^.first:=FreeBlock(s^.first); { уничтожение блоков } Dispose(s); { уничтожение дескриптора } end; { Procedure DispStr } {** Определение длины строки, длина выбирается из дескриптора } Function LenStr(s : varstr) : longint; begin LenStr:=s^.len; end; { Function LenStr } {** Присваивание строк s1:=s2 } Procedure CopyStr(s1, s2 : varstr); var bi1, bi2 : word; { индексы символов в блоках для s1 и s2 } cp1, cp2 : _bptr; { адреса текущих блоков для s1 и s2 } pp : _bptr; { адрес предыдущего блока для s1 } begin cp1:=s1^.first; pp:=nil; cp2:=s2^.first; if s2^.len=0 then begin { если s2 пустая, освобождается вся s1 } s1^.first:=FreeBlock(s1^.first); s1^.last:=nil; end else begin while cp2<>nil do begin { перебор блоков s2 } if cp1=nil then begin { если в s1 больше нет блоков } { выделяется новый блок для s1 } cp1:=NewBlock; if s1^.first=nil then s1^.first:=cp1 else if pp<>nil then pp^.next:=cp1; end; cp1^:=cp2^; { копирование блока } { к следующему блоку } pp:=cp1; cp1:=cp1^.next; cp2:=cp2^.next; end; { while } s1^.last:=pp; { последний блок } { если в s1 остались лишние блоки - освободить их } pp^.next:=FreeBlock(pp^.next); end; { else } s1^.len:=s2^.len; end; { Procedure CopyStr } {** Сравнение строк - возвращает: 0, если s1=s2; 1 - если s1 > s2; -1 - если s1 < s2 } Function CompStr(s1, s2 : varstr) : integer; var bi1, bi2 : word; cp1, cp2 : _bptr; begin cp1:=s1^.first; cp2:=s2^.first; bi1:=cp1^.i1; bi2:=cp2^.i1; { цикл, пока не будет достигнут конец одной из строк } while (cp1<>nil) and (cp2<>nil) do begin { если соответств.символы не равны, ф-ция заканчивается } if cp1^.strdata[bi1] > cp2^.strdata[bi2] then begin CompStr:=1; Exit; end; if cp1^.strdata[bi1] < cp2^.strdata[bi2] then begin CompStr:=-1; Exit; end; bi1:=bi1+1; { к следующему символу в s1 } if bi1 > cp1^.i2 then begin cp1:=cp1^.next; bi1:=cp1^.i1; end;
bi2:=bi2+1; { к следующему символу в s2 } if bi2 > cp2^.i2 then begin cp2:=cp2^.next; bi2:=cp2^.i1; end; end; { мы дошли до конца одной из строк, строка меньшей длины считается меньшей } if s1^.len < s2^.len then CompStr:=-1 else if s1^.len > s2^.len then CompStr:=1 else CompStr:=0; end; { Function CompStr } . . END.
Чтобы не перегружать программный пример, в него не включены средства повышения эффективности работы с памятью. Такие средства включаются в операции по выбору программиста. Обратите внимание, например, что в процедуре, связанной с копированием данных (CopyStr) у нас копируются сразу целые блоки. Если в блоке исходной строки были неиспользуемые места, то они будут и в блоке результирующей строки. Посимвольное копирование позволило бы устранить избыток памяти в строке-результате. Оптимизация памяти, занимаемой данными строки может производится как слиянием соседних полупустых блоков, так и полным уплотнением данных. В дескриптор строки может быть введено поле - количество блоков в строке. Зная общее количество блоков и длину строки можно при выполнении неко- торых операций оценивать потери памяти и выполнять уплотнение, если эти потери превосходят какой-то установленный процент.
Структура односвязного списка
Рисунок5.1. Структура односвязного списка

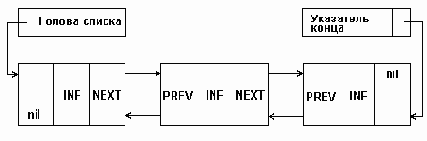
Однако, обработка односвязного списка не всегда удобна, так как отсутствует возможность продвижения в противоположную сторону. Такую возможность обеспечивает двухсвязный список, каждый элемент которого содержит два указателя: на следующий и предыдущий элементы списка. Структура линейного двухсвязного списка приведена на рис. 5.2, где поле NEXT - указатель на следующий элемент, поле PREV - указатель на предыдущий элемент. В крайних элементах соответствующие указатели должны содержать nil, как и показано на рис. 5.2.
Для удобства обработки списка добавляют еще один особый элемент - указатель конца списка. Наличие двух указателей в каждом элементе усложняет список и приводит к дополнительным затратам памяти, но в то же время обеспечивает более эффективное выполнение некоторых операций над списком.
Структура двухсвязного списка
Рисунок5.2. Структура двухсвязного списка
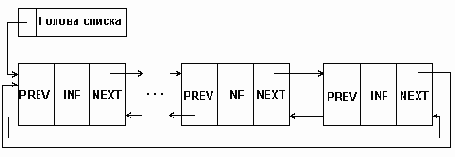
Разновидностью рассмотренных видов линейных списков является кольцевой список, который может быть организован на основе как односвязного, так и двухсвязного списков. При этом в односвязном списке указатель последнего элемента должен указывать на первый элемент; в двухсвязном списке в первом и последнем элементах соответствующие указатели переопределяются, как показано на рис.5.3.
При работе с такими списками несколько упрощаются некоторые процедуры, выполняемые над списком. Однако, при просмотре такого списка следует принять некоторых мер предосторожности, чтобы не попасть в бесконечный цикл.
Структура кольцевого двухсвязного списка
Рисунок5.3. Структура кольцевого двухсвязного списка
В памяти список представляет собой совокупность дескриптора и одинаковых по размеру и формату записей, размещенных произвольно в некоторой области памяти и связанных друг с другом в линейно упорядоченную цепочку с помощью указателей. Запись содержит информационные поля и поля указателей на соседние элементы списка, причем некоторыми полями информационной части могут быть указатели на блоки памяти с дополнительной информацией, относящейся к элементу списка. Дескриптор списка реализуется в виде особой записи и содержит такую информацию о списке, как адрес начала списка, код структуры, имя списка, текущее число элементов в списке, описание элемента и т.д., и т.п. Дескриптор может находиться в той же области памяти, в которой располагаются элементы списка, или для него выделяется какое-нибудь другое место.
Вставка элемента в середину 1-связного списка
Рисунок5.4. Вставка элемента в середину 1-связного списка
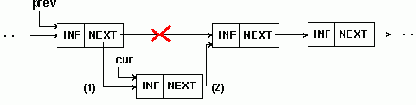 {==== Программный пример 5.2 ====} { Вставка элемента в середину 1-связного списка } Procedure InsertSll(prev : sllptr; inf : data); { prev - адрес предыдущего эл-та; inf - данные нового эл-та } var cur : sllptr; { адрес нового эл-та } begin { выделение памяти для нового эл-та и запись в его инф.часть } New(cur); cur^.inf:=inf; cur^.next:=prev^.next; { эл-т, следовавший за предыдущим теперь будет следовать за новым } prev^.next:=cur; { новый эл-т следует за предыдущим } end;
{==== Программный пример 5.2 ====} { Вставка элемента в середину 1-связного списка } Procedure InsertSll(prev : sllptr; inf : data); { prev - адрес предыдущего эл-та; inf - данные нового эл-та } var cur : sllptr; { адрес нового эл-та } begin { выделение памяти для нового эл-та и запись в его инф.часть } New(cur); cur^.inf:=inf; cur^.next:=prev^.next; { эл-т, следовавший за предыдущим теперь будет следовать за новым } prev^.next:=cur; { новый эл-т следует за предыдущим } end;
Рисунок 5.5 представляет вставку в двухсвязный список.
Вставка элемента в середину 2-связного списка
Рисунок5.5. Вставка элемента в середину 2-связного списка
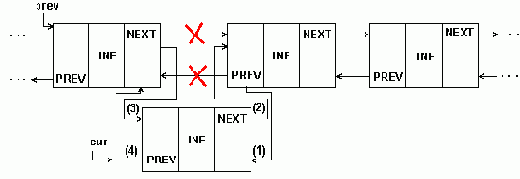
Приведенные примеры обеспечивают вставку в середину списка, но не могут быть применены для вставки в начало списка. При последней должен модифицироваться указатель на начало списка, как показано на рис.5.6.
Вставка элемента в начало 1-связного списка
Рисунок5.6. Вставка элемента в начало 1-связного списка
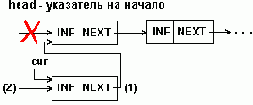
Программный пример 5.3 представляет процедуру, выполняющую вставку элемента в любое место односвязного списка.
{==== Программный пример 5.3 ====} { Вставка элемента в любое место 1-связного списка } Procedure InsertSll var head : sllptr; { указатель на начало списка, может измениться в процедуре, если head=nil - список пустой } prev : sllptr; { указатель на эл-т, после к-рого делается вставка, если prev-nil - вставка перед 1-ым эл-том } inf : data { - данные нового эл-та } var cur : sllptr; { адрес нового эл-та } begin { выделение памяти для нового эл-та и запись в его инф.часть } New(cur); cur^.inf:=inf; if prev <> nil then begin { если есть предыдущий эл-т - вставка в середину списка, см. прим.5.2 } cur^.next:=prev^.next; prev^.next:=cur; end else begin { вставка в начало списка } cur^.next:=head; { новый эл-т указывает на бывший 1-й эл-т списка; если head=nil, то новый эл-т будет и последним эл-том списка } head:=cur; { новый эл-т становится 1-ым в списке, указатель на начало теперь указывает на него } end; end;
Удаление элемента из 1-связного списка
Рисунок5.7. Удаление элемента из 1-связного списка
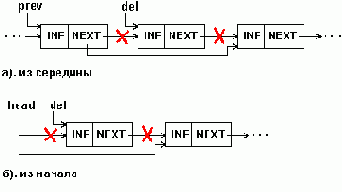
Очевидно, что процедуру удаления легко выполнить, если известен адрес элемента, предшествующего удаляемому (prev на рис.5.7.а). Мы, однако, на рис. 5.7 и в примере 5.4 приводим процедуру для случая, когда удаляемый элемент задается своим адресом (del на рис.5.7). Процедура обеспечивает удаления как из середины, так и из начала списка.
{==== Программный пример 5.4 ====} { Удаление элемента из любого места 1-связного списка } Procedure DeleteSll( var head : sllptr; { указатель на начало списка, может измениться в процедуре } del : sllptr { указатель на эл-т, к-рый удаляется } ); var prev : sllptr; { адрес предыдущего эл-та } begin if head=nil then begin { попытка удаления из пустого списка асценивается как ошибка (в последующих примерах этот случай учитываться на будет) } Writeln('Ошибка!'); Halt; end; if del=head then { если удаляемый эл-т - 1-й в списке, то следующий за ним становится первым } head:=del^.next else begin { удаление из середины списка }
{ приходится искать эл-т, предшествующий удаляемому; поиск производится перебором списка с самого его начала, пока не будет найдет эл-т, поле next к-рого совпадает с адресом удаляемого элемента }
prev:=head^.next; while (prev^.next<>del) and (prev^.next<>nil) do prev:=prev^.next; if prev^.next=nil then begin
{ это случай, когда перебран весь список, но эл-т не найден, он отсутствует в списке; расценивается как ошибка (в последующих примерах этот случай учитываться на будет) }
Writeln('Ошибка!'); Halt; end; prev^.next:=del^.next; { предыдущий эл-т теперь указывает на следующий за удаляемым } end; { элемент исключен из списка, теперь можно освободить занимаемую им память } Dispose(del); end;
Удаление элемента из двухсвязного списка требует коррекции большего числа указателей, как показано на рис.5.8.
Удаление элемента из 2-связного списка
Рисунок5.8. Удаление элемента из 2-связного списка
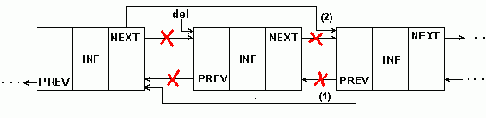
Процедуру удаления элемента из двухсвязного списка окажется даже проще, чем для односвязного, так как в ней не нужен поиск предыдущего элемента, он выбирается по указателю назад.
Перестановка соседних элементов 1-связного списка
Рисунок5.9. Перестановка соседних элементов 1-связного списка

{==== Программный пример 5.5 ====} { Перестановка двух соседних элементов в 1-связном списке } Procedure ExchangeSll( prev : sllptr { указатель на эл-т, предшествующий переставляемой паре } ); var p1, p2 : sllptr; { указатели на эл-ты пары } begin p1:=prev^.next; { указатель на 1-й эл-т пары } p2:=p1^.next; { указатель на 2-й эл-т пары } p1^.next:=p2^.next; { 1-й элемент пары теперь указывает на следующий за парой } p2^.next:=p1; { 1-й эл-т пары теперь следует за 2-ым } prev^.next:=p2; { 2-й эл-т пары теперь становится 1-ым } end;
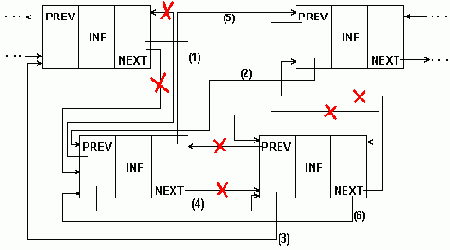
В процедуре перестановки для двухсвязного списка (рис.5.10.) нетрудно учесть и перестановку в начале/конце списка.
Перестановка соседних элементов 2-связного списка
Рисунок5.10. Перестановка соседних элементов 2-связного списка
Копирование для односвязного списка показано в программном примере 5.6.
{==== Программный пример 5.6 ====} { Копирование части 1-связного списка. head - указатель на начало копируемой части; num - число эл-тов. Ф-ция возвращает указатель на список-копию } Function CopySll ( head : sllptr; num : integer) : sllptr; var cur, head2, cur2, prev2 : sllptr; begin if head=nil then { исходный список пуст - копия пуста } CopySll:=nil else begin cur:=head; prev2:=nil; { перебор исходного списка до конца или по счетчику num } while (num>0) and (cur<>nil) do begin { выделение памяти для эл-та выходного списка и запись в него информационной части } New(cur2); cur2^.inf:=cur^.inf; { если 1-й эл-т выходного списка - запоминается указатель на начало, иначе - записывается указатель в предыдущий элемент } if prev2<>nil then prev2^.next:=cur2 else head2:=cur2; prev2:=cur2; { текущий эл-т становится предыдущим } cur:=cur^.next; { продвижение по исходному списку } num:=num-1; { подсчет эл-тов } end; cur2^.next:=nil; { пустой указатель - в последний эл-т выходного списка } CopySll:=head2; { вернуть указатель на начало вых.списка } end; end;
Пример мультисписка
Рисунок5.11. Пример мультисписка
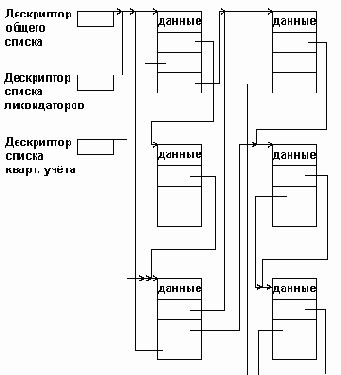
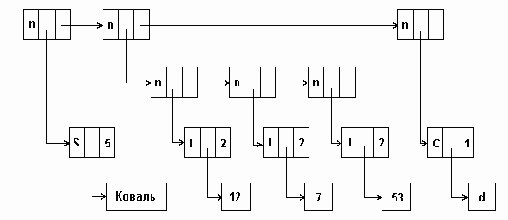
Для того, чтобы при выборке каждого подмножества не выполнять полный просмотр с отсеиванием записей, к требуемому подмножеству не относящихся, в каждую запись включаются дополнительные поля ссылок, каждое из которых связывает в линейный список элементы соответствующего подмножества. В результате получается многосвязный список или мультисписок, каждый элемент которого может входить одновременно в несколько односвязных списков. Пример такого мультисписка для названной нами автоматизированной системы показан на рис.5.11.
К достоинствам мультисписков помимо экономии памяти (при множестве списков информационная часть существует в единственном экземпляре) следует отнести также целостность данных - в том смысле, что все подзадачи работают с одной и той же версией информационной части и изменения в данных, сделанные одной подзадачей немедленно становятся доступными для другой подзадачи.
Каждая подзадача работает со своим подмножеством как с линейным списком, используя для этого определенное поле связок. Специфика мультисписка проявляется только в операции исключения элемента из списка. Исключение элемента из какого-либо одного списка еще не означает необходимости удаления элемента из памяти, так как элемент может оставаться в составе других списков. Память должна освобождаться только в том случае, когда элемент уже не входит ни в один из частных списков мультисписка. Обычно задача удаления упрощается тем, что один из частных списков является главным - в него обязательно входят все имеющиеся элементы. Тогда исключение элемента из любого неглавного списка состоит только в переопределении указателей, но не в освобождении памяти. Исключение же из главного списка требует не только освобождения памяти, но и переопределения указателей как в главном списке, так и во всех неглавных списках, в которые удаляемый элемент входил.
Граф неориентированный (а) и ориентированный (б).
Рисунок6.1. Граф неориентированный (а) и ориентированный (б).
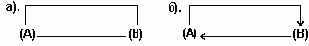
Для ориентированного графа число ребер, входящих в узел, называется полустепенью захода узла, выходящих из узела -полустепенью исхода. Количество входящих и выходящих ребер может быть любым, в том числе и нулевым. Граф без ребер является нуль-графом.
Если ребрам графа соответствуют некоторые значения, то граф и ребра называются взвешенными. Мультиграфом называется граф, имеющий параллельные (соединяющие одни и те же вершины) ребра, в противном случае граф называется простым.
Путь в графе - это последовательность узлов, связанных ребрами; элементарным называется путь, в котором все ребра различны, простым называется путь, в котором все вершины различны. Путь от узла к самому себе называется циклом, а граф, содержащий такие пути - циклическим.
Два узла графа смежны, если существует путь от одного из них до другого. Узел называется инцидентным к ребру, если он является его вершиной, т.е. ребро направлено к этому узлу.
Логически структура-граф может быть представлена матрицей смежности или матрицей инцидентности.
Матрицей смежности для n узлов называется квадратная матрица adj порядка n. Элемент матрицы a(i,j) равен 1, если узел j смежен с узлом i (есть путь < i,j >), и 0 -в противном случае (рис.6.2).
Графа и его матрица смежности
Рисунок6.2. Графа и его матрица смежности
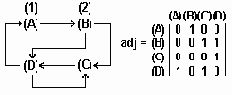
Если граф неориентирован, то a(i,j)=a(j,i), т.е. матрица симметрична относительно главной диагонали.
Матрицы смежности используются при построении матриц путей, дающих представление о графе по длине пути: путь длиной в 1 - смежный участок - , путь длиной 2 - (< A,B >,< B,C >), ... в n смежных участков: где n - максимальная длина, равная числу узлов графа. На рис.6.3 даны путевые матирцы пути adj2, adj3, adj4 для графа рис.6.2.
Матрицы путей
Рисунок6.3. Матрицы путей
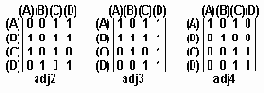
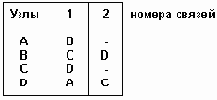
Матрицы инцидентности используются только для орграфов. В каждой строке содержится упорядоченная последовательность имен узлов, с которыми данный узел связан ориетрированными (исходящими) ребрами. На рис.6.4 показана матрица инцидентности для графа рис. 6.2.
Матрицы инцидентности
Рисунок6.4. Матрицы инцидентности
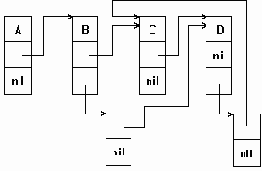
Машинное представление графа элементами двух типов
Рисунок6.5. Машинное представление графа элементами двух типов
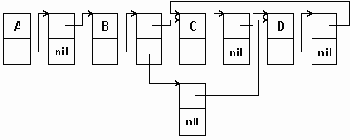
Более рационально представлять граф элементами одного формата, двойными: атом-указатель и указатель-указатель или тройными: указатель-data/down-указатель (см.раздел 5.5). На рис.6.6 тот же граф представлен элементами одного формата.
Машинное представление графа однотипными элементами
Рисунок6.6. Машинное представление графа однотипными элементами
Многосвязная структура - граф - находит широкое применение при организации банков данных, управлении базами данных, в системах программного иммитационного моделирования сложных комплексов, в системах исскуственного интеллекта, в задачах планирования и в других сферах. Алгоритмы обработки нелинейных разветвленных списков, к которым могут быть отнесены и графы, даны в разделе 5.5.
В качестве примера приведем программу, находящую кратчайший путь между двумя указанными вершинами связного конечного графа.
Пусть дана часть каpты доpожной сети и нужно найти наилучший маpшpут от города 1 до города 5. Такая задача выглядит достаточно пpостой, но "наилучший" маpшpут могут опpеделять многие фактоpы. Например: (1) pасстояние в километpах; (2) вpемя пpохождения маpшpута с учетом огpаничений скоpости; (3) ожидаемая пpодолжительность поездки с учетом доpожных условий и плотности движения; (4) задеpжки, вызванные пpоездом чеpез гоpода или объездом гоpодов; (5) число гоpодов, котоpое необходимо посетить, напpимеp, в целях доставки гpузов. Задачи о кpатчайших путях относятся к фундаментальным задачам комбинатоpной оптимизации.
Сpеди десятков алгоpитмов для отыскания кpатчайшего пути один из лучших пpинадлежит Дейкстpе. Алгоpитм Дейкстpы, опpеделяющий кpатчайшее pасстояние от данной веpшины до конечной, легче пояснить на пpимеpе. Рассмотpим гpаф, изобpаженный на pис.6.7, задающий связь между гоpодами на каpте доpог. Пpедставим гpаф матpицей смежности A, в котоpой: A(i,j)-длина pебpа между узлами i и j. Используя полученную матрицу и матрицы, отражающие другие факторы, можно определить кратчайший путь.
Часть дорожной карты, представленная в виде взвешенного графа и его матрицы смежности
Рисунок6.7. Часть дорожной карты, представленная в виде взвешенного графа и его матрицы смежности
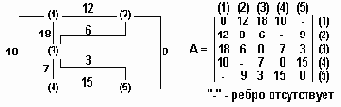 {========== Программный пример 6.1 ==============} { Алгоритм Дейкстры } Program ShortWay; Const n=5; max=10000; Var a: Array [1..n,1..n] of Integer; v0,w,edges: Integer; from,tu,length: Array [1..n] of Integer; Procedure adjinit; { Эта пpоцедуpа задает веса pебеp гpафа посpедством опpеделения его матpицы смежности A pазмеpом N x N } Var i,j: Integer; Begin { "Обнуление" матpицы (веpшины не связаны) } For i:=1 to n do For j:=1 to n do a[i,j]:=max; For i:=1 to n do a[i,i]:=0; { Задание длин pебеp, соединяющих смежные узлы гpафа } a[1,2]:=12; a[1,3]:=18; a[1,4]:=10; a[2,1]:=12; a[2,3]:=6; a[2,5]:=9; a[3,1]:=18; a[3,2]:=6; a[3,4]:=7; a[3,5]:=3; a[4,1]:=10; a[4,3]:=7; a[4,5]:=15; a[5,2]:=9; a[5,3]:=3; a[5,4]:=15; End; Procedure printmat; { Эта пpоцедуpа выводит на экpан дисплея матpицу смежности A взвешенного гpафа } Var i,j: Integer; Begin writeln; writeln('Матpица смежности взвешенного гpафа (',n,'x',n,'):'); writeln; For i:=1 to n do Begin write ('Ё'); For j:=1 to n do If a[i,j]=max Then write(' ----') Else write(a[i,j]:6); writeln(' Ё') End; writeln; writeln (' ("----" - pебpо отсутствует)') End; Procedure dijkst;
{========== Программный пример 6.1 ==============} { Алгоритм Дейкстры } Program ShortWay; Const n=5; max=10000; Var a: Array [1..n,1..n] of Integer; v0,w,edges: Integer; from,tu,length: Array [1..n] of Integer; Procedure adjinit; { Эта пpоцедуpа задает веса pебеp гpафа посpедством опpеделения его матpицы смежности A pазмеpом N x N } Var i,j: Integer; Begin { "Обнуление" матpицы (веpшины не связаны) } For i:=1 to n do For j:=1 to n do a[i,j]:=max; For i:=1 to n do a[i,i]:=0; { Задание длин pебеp, соединяющих смежные узлы гpафа } a[1,2]:=12; a[1,3]:=18; a[1,4]:=10; a[2,1]:=12; a[2,3]:=6; a[2,5]:=9; a[3,1]:=18; a[3,2]:=6; a[3,4]:=7; a[3,5]:=3; a[4,1]:=10; a[4,3]:=7; a[4,5]:=15; a[5,2]:=9; a[5,3]:=3; a[5,4]:=15; End; Procedure printmat; { Эта пpоцедуpа выводит на экpан дисплея матpицу смежности A взвешенного гpафа } Var i,j: Integer; Begin writeln; writeln('Матpица смежности взвешенного гpафа (',n,'x',n,'):'); writeln; For i:=1 to n do Begin write ('Ё'); For j:=1 to n do If a[i,j]=max Then write(' ----') Else write(a[i,j]:6); writeln(' Ё') End; writeln; writeln (' ("----" - pебpо отсутствует)') End; Procedure dijkst;
{ Эта пpоцедуpа опpеделяет кpатчайшее pасстояние от начальной веpшины V0 до конечной веpшины W в связном гpафе с неотpицательными весами с помощью алгоpитма, пpинадлежащего Дейкстpе.
Результатом pаботы этой пpоцедуpы является деpево кpатчайших путей с коpнем V0.
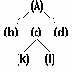
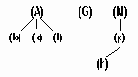
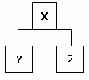

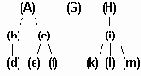

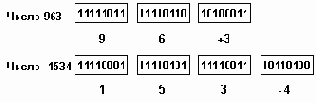


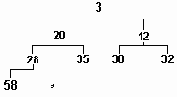
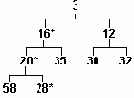
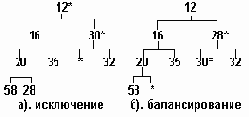




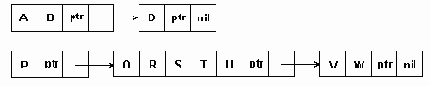




 {==== Программный пример 5.2 ====} { Вставка элемента в середину 1-связного списка } Procedure InsertSll(prev : sllptr; inf : data); { prev - адрес предыдущего эл-та; inf - данные нового эл-та } var cur : sllptr; { адрес нового эл-та } begin { выделение памяти для нового эл-та и запись в его инф.часть } New(cur); cur^.inf:=inf; cur^.next:=prev^.next; { эл-т, следовавший за предыдущим теперь будет следовать за новым } prev^.next:=cur; { новый эл-т следует за предыдущим } end;
{==== Программный пример 5.2 ====} { Вставка элемента в середину 1-связного списка } Procedure InsertSll(prev : sllptr; inf : data); { prev - адрес предыдущего эл-та; inf - данные нового эл-та } var cur : sllptr; { адрес нового эл-та } begin { выделение памяти для нового эл-та и запись в его инф.часть } New(cur); cur^.inf:=inf; cur^.next:=prev^.next; { эл-т, следовавший за предыдущим теперь будет следовать за новым } prev^.next:=cur; { новый эл-т следует за предыдущим } end;







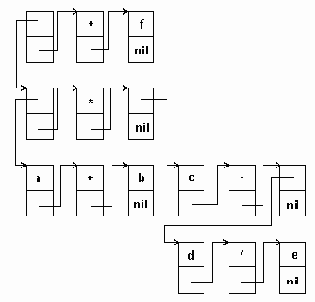 Выражение: (a+b)*(c-(d/e))+f будет вычисляться в следующем порядке: a+b d/e c-(d/e) (a+b)*(c-d/e) (a+b)*(c-d/e)+f
Выражение: (a+b)*(c-(d/e))+f будет вычисляться в следующем порядке: a+b d/e c-(d/e) (a+b)*(c-d/e) (a+b)*(c-d/e)+f


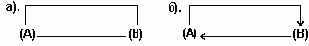
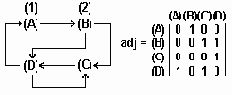
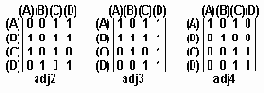



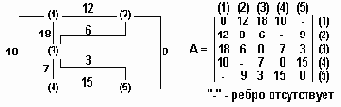 {========== Программный пример 6.1 ==============} { Алгоритм Дейкстры } Program ShortWay; Const n=5; max=10000; Var a: Array [1..n,1..n] of Integer; v0,w,edges: Integer; from,tu,length: Array [1..n] of Integer; Procedure adjinit; { Эта пpоцедуpа задает веса pебеp гpафа посpедством опpеделения его матpицы смежности A pазмеpом N x N } Var i,j: Integer; Begin { "Обнуление" матpицы (веpшины не связаны) } For i:=1 to n do For j:=1 to n do a[i,j]:=max; For i:=1 to n do a[i,i]:=0; { Задание длин pебеp, соединяющих смежные узлы гpафа } a[1,2]:=12; a[1,3]:=18; a[1,4]:=10; a[2,1]:=12; a[2,3]:=6; a[2,5]:=9; a[3,1]:=18; a[3,2]:=6; a[3,4]:=7; a[3,5]:=3; a[4,1]:=10; a[4,3]:=7; a[4,5]:=15; a[5,2]:=9; a[5,3]:=3; a[5,4]:=15; End; Procedure printmat; { Эта пpоцедуpа выводит на экpан дисплея матpицу смежности A взвешенного гpафа } Var i,j: Integer; Begin writeln; writeln('Матpица смежности взвешенного гpафа (',n,'x',n,'):'); writeln; For i:=1 to n do Begin write ('Ё'); For j:=1 to n do If a[i,j]=max Then write(' ----') Else write(a[i,j]:6); writeln(' Ё') End; writeln; writeln (' ("----" - pебpо отсутствует)') End; Procedure dijkst;
{========== Программный пример 6.1 ==============} { Алгоритм Дейкстры } Program ShortWay; Const n=5; max=10000; Var a: Array [1..n,1..n] of Integer; v0,w,edges: Integer; from,tu,length: Array [1..n] of Integer; Procedure adjinit; { Эта пpоцедуpа задает веса pебеp гpафа посpедством опpеделения его матpицы смежности A pазмеpом N x N } Var i,j: Integer; Begin { "Обнуление" матpицы (веpшины не связаны) } For i:=1 to n do For j:=1 to n do a[i,j]:=max; For i:=1 to n do a[i,i]:=0; { Задание длин pебеp, соединяющих смежные узлы гpафа } a[1,2]:=12; a[1,3]:=18; a[1,4]:=10; a[2,1]:=12; a[2,3]:=6; a[2,5]:=9; a[3,1]:=18; a[3,2]:=6; a[3,4]:=7; a[3,5]:=3; a[4,1]:=10; a[4,3]:=7; a[4,5]:=15; a[5,2]:=9; a[5,3]:=3; a[5,4]:=15; End; Procedure printmat; { Эта пpоцедуpа выводит на экpан дисплея матpицу смежности A взвешенного гpафа } Var i,j: Integer; Begin writeln; writeln('Матpица смежности взвешенного гpафа (',n,'x',n,'):'); writeln; For i:=1 to n do Begin write ('Ё'); For j:=1 to n do If a[i,j]=max Then write(' ----') Else write(a[i,j]:6); writeln(' Ё') End; writeln; writeln (' ("----" - pебpо отсутствует)') End; Procedure dijkst;