Числа и переменные
В математических выражениях ССМ МС5 могут использоваться следующие представления чисел:
действительные числа с фиксированным десятичным знаком – например, сопротивление 5,6 кОм представляется как 5600 или 5.6 К. Отметим, что в качестве десятичного знака используется точка;
действительные числа с плавающим десятичным знаком — научная нотация. Например, емкость 1 мкФ может быть представлена как 1Е-6;
действительные числа с плавающим десятичным знаком — инженерная нотация, согласно которой различные степени 10 обозначаются следующими суффиксами:

Для экономии места на графиках малая буква "m" обозначает 10-3, большая буква "М" — 106.
При представлении чисел большие и малые буквы не различаются. Например, сопротивление 1,8 МОм может быть записано как 1.8MEG, 1.8mеg или 1800К. Пробелы между числом и буквенным суффиксом не допускаются!
В ССМ МС5 ряд констант и переменных имеют стандартные значения:
GMIN — минимальная проводимость ветви, задаваемая в диалоговом окне Options - Global settings;
PI — число =3.14159265389795;
TEMР — температура компонентов в градусах Цельсия;
VT — температурный потенциал р-п перехода, равный 1,3806226-10-23* (273,15+ТЕМР)/(1,6021918-10-19); при ТЕМР=27 °C VT=25,86419 мВ.
Номера узлов, присваиваемые программой МС5 автоматически, представ-ляют собой целые числа, например 3, 12, 27. Кроме того, пользователь может присвоить любому узлу имя в виде текстовой алфавитно-цифровой переменной, начинающейся с буквы или символа "_" и содержащей не более 50 символов, например, А1, Input, Земля.
В математических выражениях используются следующие переменные:

В этом перечне символы А и В обозначают номера узлов схемы, D1 — имя компонента с двумя выводами или управляемого источника, Q1 — имя любого активного устройства или линии передачи. Символы R и S заменяются аббревиатурами выводов устройств согласно следующей таблице:

Например, следующие выражения означают: I(R3) —ток через резистор R3; R(RВЫХ) — сопротивление резистора RВЫХ; L(LK) – индуктивность катушки LK; IB(VT1) — ток базы биполярного транзистора VT1; VCE(Q1) - напряжение между коллектором и эмиттером биполярного транзистора Q1.
Добавление в библиотеку компонентов и редактирование их параметров
Очень часто возникает необходимость редактировать параметры компонентов в новой или существующей библиотеке, поэтому на Рис. 2.5. показано диалоговое окно, открывающееся после выбора имени библиотеки на Рис 2.4. В этом окне можно редактировать параметры существующих компонентов и добавлять новые компоненты.
Для установки соответствия между компонентами библиотеки и их отображением на схеме применяется диалоговое окно редактора компонентов Component Editor (Рис. 2.6.), вызываемое командой меню Windows->Component Editor.
Для создания нового компонента выбирается имя группы (в правом окне Component Editor, см. Рис 2.6.), в которой он должен быть расположен, и нажимается кнопка Add Component (Добавить компонент). Образуется новый компонент с именем new_1, new_2 и т.д. После этого заполняются поля текстовой информации и включаются необходимые опции, определяющие, будет или не будет виден атрибут компонента при редактировании схемы в редакторе схем. Каждому новому компоненту присваивается уникальное имя, указывается имя УГО (после этого изображение символа в левом окне принимает необходимый вид, причём названия УГО, кончающиеся приставкой _Euro, описывают УГО, близкие к российскому ГОСТу), указывается имя математической модели, начальное расположение позиционного обозначения и расположение имен выводов. Если компонент является макромоделью (Macro, Subckt), логическим выражением (Logic Expression), устройством задержки сигналов (Pin Delay) или устройством контроля (Constraints), необходимо дополнительно ввести выводы и присвоить им имена. Для этого щелчком мыши в окне символа отмечают расположение точки вывода и в открывшемся окне (Рис. 2.7.) указывают его имя и тип: Analog — аналоговый, Digital — цифровой (по умолчанию устанавливается тип Analog).
Для создания новой группы в списке компонентов курсор подводится к имени группы предыдущего уровня иерархии и нажимается кнопка Add Group (Добавить группу). Созданной группе автоматически присваивается имя New Group (Новая группа), которое затем может быть изменено в открывшемся в левой части экрана окне Group (Группы).
Например, для создания в группе Analog Library библиотеки отечественных компонентов курсором выбираем имя этой группы, нажимаем на кнопку Add Group и в окне Group заменяем стандартное имя New Group на Russian или любое другое (см. Рис. 2.6.). Вновь образовавшаяся группа занимает последнее место в списке групп данного уровня иерархии.

Рис.2.6. Добавление компонента в окне редактора компонентов Component Editor

Рис 2.7. Редактирование имени и типа вывода
Для редактирования условных графических отображений компонентов используется диалоговое окно Shape Editor, вызываемое командой меню Windows->Shape Editor. В появившемся окне ( Рис. 2.8) можно поставить в соответствие электронным компонентам, содержащимся в библиотеке программы, их графическое отображение в окне редактора схемы (см. [4]).

Рис.2.8. Диалоговое окно редактора условных графических обозначений Shape Editor



Главное окно программы
Главное окно с содержанием основного меню программы приведено на рис. 2.1. На этом рисунке также кратко указано назначение основных элементов окна, не требующих дополнительных разъяснений. В системе схемотехнического моделирования (ССМ) МС5 используется стандартный для ОС Windows многооконный интерфейс с ниспадающими и разворачивающимися окнами - меню.
Так ниже приведено содержание окна кнопки системного меню ( самое левое верхнее поле ). Системное меню используется для управления характеристиками окна с клавиатуры и обеспечивает следующие стандартные команды Windows:


Рис. 2.1. Главное окно и основное меню программы

Далее приведено также содержание кнопки меню управления окном схемы. Используя указанные кнопки с помощью мыши легко выходить из окна схем в главное меню и из окна главного меню в операционную систему.
Меню управления окном схемы размещается в верхнем левом углу окна схемы и включает следующие команды :




Copyright © 2000 Георгий Долин. All rights reserved. Design - "Kety studio" by Alex Kazantsev. Support - "Anri Education Systems"
Меню главного окна или меню команд МС5 представлено на рис. 2.1 второй строчкой сверху. Оно состоит из команд File, Edit, Components, Windows, Options, Analysis, Help. Ряд команд выполняется немедленно после их выбора, в то время как содержащие многоточие "…" требуют ввода дополнительной информации, а имеющие знак 4указывают на то, что дополнительное меню разворачивается вправо. Рассмотрим меню основных команд главного окна.
Меню File служит для загрузки, создания и сохранения файлов схем, файлов библиотек математических моделей компонентов схем а также для вывода схем на принтер или плоттер.

Команда Component главного меню программы используется для добавления в создаваемую или редактируемую схему новых компонентов. Команда Component содержит каталог более 100 аналоговых и цифровых компонентов электрических схем (фактически, имена компонентов).
Иерархическое построение каталога позволяет достаточно быстро вызвать требуемый компонент схемы. Коммерческая версия содержит более 7000 моделей компонентов. В этом случае наиболее часто применяемые компоненты можно поместить на Панель инструментов (см. текст в конце данного раздела) в виде кнопок УГО компонентов. Для убыстрения поиска и выбора компонентов можно использовать и 4 палитры компонентов (см. описание команды Options). Десять наиболее часто используемых компонентов автоматически отображаются в списке Last Used в конце меню команды Component.
Каталог команды Component можно редактировать, в том числе создавать новые разделы иерархии и вводить в них новые компоненты, например, отечественного производства. Для этого используется команда Component Editor из подменю команды Windows главного меню. Меню команды Component приведено ниже

Меню Options используется для настройки параметров программы.



Меню команды Windows главного окна позволяет манипулировать открытыми окнами и обеспечивает доступ к редакторам ССМ MCV и калькулятору этой программы.

Меню Analysis позволяет выбрать вид анализа

- Го занятия
|
|
|
|
|
|
|
|
И дифференцирующей RC цепочек»
Цель работы: изучить способы создания схем в редакторе МСV, основные виды анализа схем и способы оценки результатов анализа схем. Ознакомиться с основными электрическими характеристиками интегрирующей и дифференцирующей цепочек.
“Исследование КПУ на основе эквивалентной схемы УЭ с ИТУН”
Цель работы : изучить способ использования ИТУН для получения экви-валентной схемы БТ(ПТ и ЭЛ) и моделирования КПУ; практически освоить проведение основных видов анализа схемы и оценки результатов её анализа; ознакомиться с основными характеристиками КПУ и сопоставить их с теоретическими положениями.
Цель работы: изучить способы использования ИТУТ для получения эквивалентной схемы БТ и моделирования КПУ; практически освоить проведение основных видов анализа схемы и оценку результатов её анализа; ознакомиться с основными характеристиками КПУ и сопоставить их с теоретическими положениями.
“ Исследование зависимых источников, управляемых преобразователем Лапласа”
Цель работы: изучить возможности моделирования сложных линейных инерционных цепей с помощью зависимых источников, управляемых преобразованием Лапласа; ознакомиться с особенностями атрибутов этих источников, с особенностями их взаимодействия с нагрузкой и сопротивлением источника сигнала.
Источник импульсного напряжения

Рис. 4.5.
УГО источника. Атрибутов в окне два: PART= «имя», например, PUL1, (PUL - нельзя); MODEL= «имя модели из библиотеки моделей» или «список параметров модели». Способы определения атрибута MODEL те же, что и для синусоидального источника (см. п. 4.2.), также как и ввод нового источника в библиотеку моделей. Обозначение параметров источника следующие:

Отметим, что с помощью этого источника можно сформировать очень разнообразные функции: единичную 1(t), импульсную d(t)-приближенно, меандр, последовательности треугольных, трапецеидальных, прямоугольных импульсов и др.
Источник напряжения, задаваемый пользователем

Рис. 4.6
Пользователь имеет возможность задать напряжение источника произвольной формы, причем отсчёты времени и напряжения, вводимые пользователем, записываются в текстовый файл. Однако гораздо чаще этот файл создается другим путем. При расчете переходных процессов в режиме Transient Analysis можно сохранить одно или несколько напряжений сигнала в текстовом файле, имя которого совпадает с именем схемы, а расширение будет .usr. Для этого в меню Transient Analysis Limits графики требуемых напряжений (или переменных) отмечаются нажатием пиктограммы

Источник синусоидального напряжения

Рис. 4.3.
Подключение + или – источника к “земле” меняет фазу напряжения источника на 1800. Параметры источника можно вводить в схему несколькими способами. Но лучше все-таки воспользоваться окном атрибутов, которое автоматически появляется в окне редактора после выбора и вывода источника, щелчком левой кнопки мыши, на экран в схему. Атрибутов в окне два: PART = “имя”, где имя определяет источник и его позиционное положение, например, PART=HA (или PART=S1 или PART=SIN2); MODEL – «список параметров модели» или «имя модели из библиотеки моделей». Определение атрибута MODEL возможно следующими способами:
Если нужно быстро провести оценочный анализ частотных характеристик схемы, то в поле атрибута MODEL можно ничего не вводить и после нажатия клавиши ОК в окне атрибутов программа сама автоматически введет параметры модели синусоидального источника напряжения по умолчанию, т.е. частоту F=1 MEG, внутреннее сопротивление RS=1E-3Ом; амплитуду напряжения А=1V. Если синусоидальный источник вводится с параметрами, необходимыми только для конкретной схемы, то параметры можно либо ввести в поле атрибута: MODEL= «список параметров модели», либо текстовой директивой как в окне текстового отображения схемы, так и в окне графического отображения схемы по формату: .model <имя модели> sin ([список параметров модели]). Этот способ неудобен тем, что пользователю необходимо помнить список параметров модели. Если источник будет использоваться в нескольких схемах, то его целесообразно ввести в библиотеку моделей компонентов. В этом случае в поле атрибута MODEL вводится лишь имя источника из библиотеки моделей, например, MODEL=GEN. При этом имя источника можно выбрать из уже имеющихся имен источников в библиотеке щелчком мыши.Список имен, имеющихся в библиотеке, высвечивается в правом поле окна атрибутов (см. Рис. 4.4.). Если же необходимо внести в библиотеку моделей новый источник с новыми параметрами, то поступают следующим образом. Для обращения к библиотеке моделей выполняют команду File и Open. В открывшемся окне «Открытие файлов» выбираем из списка Тип файлов файлы библиотеки Model Library [*.lbr]. В результате открывается список с именами имеющихся в программе библиотек. Выбрав библиотеку, щелкаем по ее имени в списке. При этом, открывается главное окно выбранной библиотеки. В левом верхнем поле, щелкнув мышью на черном треуголнике, открываем окно со списком моделей компонентов данной библиотеки. В этом окне выбираем интересующий нас компонент с именем Sinusoidal. Открывается окно с именами и параметрами синусоидальных источников напряжения. Заметим, что изложенным способом можно открыть окно с моделями любого типа компонентов, входящих в данную библиотеку (см. п. 2 пособия).
Для добавления в библиотеку нового источника синусоидального напряжения необходимо нажать кнопку Add. В левом окне с именем Name List в конце списка появляется строка с именем NEW. В правом поле параметров сразу устанавливаются параметры модели по умолчанию. В этом поле нужно устанавливать значение параметров своей модели [3,4].
Можно присвоить своему источнику синусоидального напряжения имя в библиотеке моделей, которое будет появляться в правом поле окна атрибутов (см. Рис. 4.4.). Для этого вводиться новое имя в окне NAME (слева вверху окна компонента), например GEN. Щелкнув мышью в строке NEW, переносим имя GEN в эту строку вместо NEW. После этого введенный источник можно использовать с любой схемой. Важно, что при выборе имени источника из библиотеки моделей в окне атрибутов, параметры модели источника автоматически записываются в окно текстового отображения схемы [10].

Рис. 4.4.
Заметим, что аналогично изложенному выше способу можно ввести параметры любого нового компонента из имеющихся в библиотеке моделей типов компо-нентов, например, NPN – транзистора, диода, операционного усилителя и т.д.
Обозначения параметров синусоидального источника следующие:

Источники постоянного напряжения и тока
Эти источники используются во всех видах анализа схем. Имя источника напряжения в библиотеке компонентов – Battery. Путь к имени компонента: Component и Analog Primitives и Waveform Sources и Battery. УГО источника напряжения приведено на Рис. 4.1. Внутреннее сопротивление батареи R = 0,001 Ом. Параметры батареи можно вводить в схему по текстовой директиве .define, как в MC IV, но лучше вводить с помощью окна атрибутов (как на Рис. 5.6. – Рис. 5.9. [10]). Для батареи используются два атрибута: PART = B1 (или V1,E2 и т.д.) – имя и позиционное обозначение; VALUE – «значение ЭДС источника напряжения». Например, VALUE=12V.
 Рис. 4.1 |
 Рис. 4.2 |
Имя источника тока в библиотеке компонентов – ISource. Путь к имени компонента: Component и Analog Primitives и Waveform Sources и ISource. УГО источника напряжения приведено на Рис. 4.2. Внутренняя проводимость равно Gmin, величина, которого устанавливается в меню Options в глобальных переменных. В одной схеме можно использовать несколько батарей и источников тока. Для ввода параметров источника тока используют окно с двумя атрибутами: PART = I1 (или I9 и т.д.) – имя и позиционное обозначение; VALUE – «значение тока источника». Например, VALUE=1А.



Copyright © 2000 Георгий Долин. All rights reserved. Design - "Kety studio" by Alex Kazantsev. Support - "Anri Education Systems"
Линейные зависимые источники

1. Источник тока, управляемый напряжением (ИТУН). Его УГО приведено на Рис. 3.1.
Рис.3.1. УГО ИТУН
Имя источника в библиотеке пассивных компонентов – IofV. Путь к источнику: меню Component и Analog Primitives и Dependet Sources. Все линейные источники имеют (при графическом отображении схем) два атрибута: 1) PART <имя>, где имя отображает название и позиционное положение компонента, например, I1,G3; GEN и т.д.; 2) VALUE <коэффициент передачи>. Атрибут VALUE применительно к ИТУН имеет размерность проводимости и представляет собой крутизну S. Функциональное соотношение для источника: I=SUупр . Это соотношение удобно при линейном представлении УЭ, например, ПТ и ЭЛ. Крутизна вводится в А/В. Ввести параметры источника можно либо в окне атрибутов (см. [10], Рис. 5.6 – Рис. 5.9), либо по текстовой директиве .define, причем последнее как в окне схемы, так и в окне текстового отображения схемы. При этом директива выглядит следующим образом: «.define G1 0.04». Здесь S = 40 мА/В. В MC5 лучше вводить параметры компонентов в окне атрибутов. Управляющее напряжение Uупр должно действовать на R или L.

Рис.3.2. УГО ИТУТ

Рис.3.3. УГО ИНУН

Рис.3.4. УГО ИНУТ
Линейные зависимые источники, задаваемые преобразованием Лапласа
В MC5 можно моделировать линейные четырехполюсники с помощью аналитического представления их передаточной характеристики на комплексной плоскости в виде операторного выражения от комплексной переменной S=a+jw. Это обстоятельство открывает широкие возможности для моделирования ФСС высоких порядков любого типа. Возможно также моделирование усилителей со сложными цепями ОС и коррекцией АЧХ. Операторное выражение для передаточной характеристики в MC5 присваивается линейному зависимому источнику. Таких источников в MC5 восемь и их имена начинаются с буквы L, они находятся в подменю Component->Analog Primitives->Laplace Sources меню главного окна программы. Эти источники используются при всех видах анализа. При расчете частотных характеристик (режима AC) переменная S заменяется на jw, при расчете передаточных характеристик (режим DC) S полагается равной нулю. При расчете переходных характеристик с использованием рассматриваемых источников отыскивается импульсная характеристика четырехполюсника как обратное преобразование Фурье от передаточной характеристики, а затем из свёртки импульсной характеристики с входным сигналом определяется выходной переходный процесс.
Четыре источника LTIofI, LTIofV, LTVofI и LTVofV задаются таблично и по причинам, изложенным в конце п. 3.3., здесь не рассматриваются.
Следующие четыре источника задаются функциональной зависимостью:
1. Источник тока, управляемый напряжением (ИТУН). Его имя в библиотеке компонентов LFIofV (в подменю Analog Primitives меню Component главного окна программы). УГО рассматриваемого источника приведено на Рис. 3.13.
 Рис.3.13 УГО источника LFIofV |
 Рис. 3.14 УГО источника LFIofI |
Параметры источника целесообразно задавать с помощью окна атрибутов. Используются два атрибута. Для позиционного обозначения источника в атрибуте PART используется буквенно-цифровое обозначение, например PART=G1 (см. Рис. 3.13). Второй атрибут LAPLACE используется для формульного ввода операторного выражения передаточной характеристики.
Например, дифференцирующая цепочка задается следующим выражением: LAPLACE=S/(S+1E5).
Параллельный колебательный контур может быть представлен следующим образом: LAPLACE=1E-8*S/(1E12+1E4*S+S*S).
2. Источник тока, управляемый током (ИТУТ). Имя источника в библиотеке компонентов LFIofI. УГО данного источника приведено на Рис. 3.14. Этот источник также задается с помощью двух атрибутов: позиционного, например PART=F1(см. Рис. 3.14), и формульного - LAPLACE. Например, интегрирующую цепочку можно задать следующим выражением в окне атрибутов: LAPLACE = 1/(1+1E-5*S). ФВЧ первого порядка: LAPLACE=S/(1+0.001*S) и т.д.
3. Источник напряжения, управляемый напряжением (ИНУН). Имя источника в библиотеке компонентов LFVofV. УГО источника показано на Рис. 3.15. Источник в схеме также определяется двумя атрибутами: позиционным PART=E1; и формульным – LAPLACE. Например, цепь второго порядка может быть представлена с помощью выражения: LAPLACE=1/(1+0.01*S+1E-6*S*S).
4. Источник напряжения, управляемый током (ИНУТ). Имя источника в библиотеке компонентов LFVofI. УГО источника дано на Рис. 3.16. Источник в схеме задается также двумя атрибутами, как и предыдущие: PART=H1;
 |
 |
Линейные зависимые источники, задаваемые Z-преобразованием
Программа MC5 версии 2.01 содержит четыре линейных зависимых источника, задаваемых Z-преобразованием. Точнее, само Z-преобразование в MC5 реализуется косвенно, через преобразование Лапласа, причем переменная Z определяется следующим образом: =exp(st). Тем не менее в MC5 версии 2.01 пользователь «не замечает» этой подмены преобразования, работая в Z-плоскости с Z как с самостоятельной переменной. Способы использования и реализации Z-преобразования для моделирования цифровых фильтров подробно рассмотрены в пункте 6. Здесь рассмотрим лишь линейные источники, задаваемые Z-преобразованием:
1. Источник тока, управляемый напряжением (ИТУН). Его имя в библиотеке компонентов (Component->Analog Primitives->Z Transform Sources) – ZIofV. УГО этого источника показано на Рис. 3.17. Параметры этих источников также удобно вводить в схему с помощью окна атрибутов. Для определения этих источников используются три атрибута. Первый атрибут PART – определяет
 Рис. 3.17 УГО источника ZIofV |
 Рис. 3.18 УГО источника ZIofI |
традиционное буквенно-цифровое обозначение источника, например, PART=G1 (см. Рис. 3.17). Второй атрибут ZEXP используется либо для ввода имени, с помощью которого по текстовой директиве .define (см. п.6 пособия и [4]) записывается выражение для системной функции устройства в Z-плоскости, либо для ввода указанного выражения сразу в окно атрибутов. Второй способ проще, тогда как первый способ – нагляднее. Третий атрибут CLOCK FREQUENCY служит для ввода тактовой частоты или частоты дискретизации FC. Например, атрибуты могут иметь следующие значения: PART=G1; ZEXP=ZFILTER; CLOCK FREQUENCY=24K. При этом на схеме (или в окне текстового отображения схемы) текстовой директивой должна быть введена системная функция фильтра H(z) : .define ZFILTER (.10285*(Z+1)*(POW(Z,2)-.70621*Z+1))/((Z-.55889)*(POW(Z,2)-1.1579*Z+.76494)).
Аналогичным образом с помощью указанных атрибутов вводятся и другие Z-источники. Важно отметить, что при вводе выражения для системной функции фильтра в атрибут < ZEXPression> оно должно содержать по крайней мере один экземпляр переменной Z.
2. Источник тока, управляемый током (ИТУТ). Его имя в библиотеке компонентов – ZIofI. УГО этого источника приведено на Рис. 3.18. Способ ввода параметров источника с помощью трех атрибутов изложен выше для ZIofV. Например, второй атрибут: ZEXP=1/3*(1+Z+pow(Z,2)).
3. Источник напряжения, управляемый напряжением (ИНУН). Его имя в библиотеке компонентов – ZVofV. УГО этого источника приведено на Рис. 3.19. Способ ввода параметров источника с помощью трех атрибутов изложен
 |
 |
4. Источник напряжения, управляемый током (ИНУТ). Его имя в библиотеке компонентов – ZVofI. УГО этого источника приведено на Рис. 3.20. Способ ввода параметров источника с помощью трех атрибутов изложен выше. Этот источник используется редко.
Литература
1. Попов В.П. Применение ППП Micro-CAP для автоматизированного анализа цепей/ ТРТУ.-Таганрог, 1995.-85 с.
2. Разевиг В.Д. Система схемотехнического моделирования Micro-CAP IV/МЭИ.-М., 1997.- 128с., ил.
3. Разевиг В.Д. Система схемотехнического моделирования и проектирвоания печатных плат Design Center (PSpice).-М.: СК Пресс, 1996.-272 с., ил.
4. Разевиг В.Д. Система схемотехнического проектирования Micro-CAP V.-М.: “СОЛОН”, 1997. – 273 с., ил.
5. Кубицкий А.А. Исследование оконечных бестрансформаторных УЗЧ с использованием ПЭВМ (компьютерное моделирование - лаб. работа)/ МТУСИ.-М., 1996.-17 с.
6. Кубицкий А.А. Проектирование оконечных бестрансформаторных усилителей звуковой частоты с использовнаием ПЭВМ: Учебное пособие/ МТУСИ.-М., 1998.-31 с.
7. Материалы, полученные по сети Internet: http://www.spectrum-soft.com/
8. Michael A. Wyatte. Spice воспринимает и отображает Y- параметры. –Design Ideas Supplement for EDN, June, 1995.
9. B.Al Hashimi and Moniri. Spice обеспечивает моделирование схем в Z –области.- Edition of EDN, April,1996.
10. Радиоприёмные устройства. Учебник для вузов/ Н.Н. Фомин и др. - Под ред. Н.Н. Фомина.- М.: Радио и связь, 1996. - 512 с.: ил.
11. H.Ronen, M.Eliahu, A.Harel. Преподавание и изучение основ электроники с использованием профессиональных программ анализа цепей. Европейский журнал по инженерному образованию. Том 20, №4, 1995.
12. Кубицкий А.А., Долин Г.А. Применение Micro-CAPV при проектировании радиотехнических устройств: Учебное пособие, часть I / МТУСИ.-М.:1998.-36с.
13. Баскаков С.И. Радиотехнические цепи и сигналы: Учеб. для вузов по спец. «Радиотехника».-М.:Высш. шк.,1988.-448с.: ил.
14. Горохов В.А., Стручков А.А. Микросхемотехника устройств связи на основе сигнальных микропроцнссоров. Цифровые фильтры. Часть II : Учебное пособие/ МИС.- М.,1988. 49с.
Математические операции и выражения
В сложных текстовых переменных директивы .DEFINE и при указании переменных, выводимых на графиках при проведении моделирования, можно использовать следующие математические операции.
Арифметические операции: + — сложение; - — вычитание; * — умножение; /—деление; MOD — остаток после целочисленного деления; DIV — целочисленное деление
Тригонометрические функции от действительных и комплексных величин (х —действительная, z — комплексная величина): Ехр(х) — экспонента; Ln(х) — натуральный логарифм; Log(z) — десятичный логарифм; Sin(z) – синус; Cos(x) – косинус; Tan(x) – тангенс; Asin(x) – арксинус; Acos(x) – арккосинус; Atn(x) –арктангенс; SINH(z) – гиперболический синус; COSH(z) – гиперболический косинус; TANH(z) – гиперболический тангенс; COTH(z) – гиперболический котангенс.
Другие функции от действительных и комплексных величин: Abs(z) – абсолютное значение; Sqrt(z) – корень квадратный из модуля z; Sgn(x) – знак числа; POW(Z,X) – степень ZX = e Xln(Z) ; SUM(u,t) – текущий интеграл от переменной u по переменной t; RMS(u) – текущее среднеквадратическое отклонение переменной u при интегрировании по времени t;AVG(u) – текущее среднее значение переменной u ; DEL(u) – приращение процесса u относительно предыдущей точки при расчете переходных процессов. Производная рассчитывается как отношение двух таких операторов, например, производная du/dt равна DEL(u)/DEL(t); IМРОRТ(имя файла,у) – импорт функции y из файла. В текстовом файле помещается таблица значений переменных, в качестве которых может быть время (T), частота (F), напряжение источника напряжений (V(имя источника)), ток источника тока (I(имя источника)), и выражение для у и другие [3,4].
Операции отношения и логические операции: = – равно; > – больше; < – меньше; >= – больше или равно; <= – меньше или равно; <> – не равно; AND – логическое И; NAND – отрицание логического И; NOT – отрицание; OR – логическое ИЛИ; NOR – отрицание логического ИЛИ; XOR – исключающее ИЛИ.
Функции от комплексных чисел: DB(z) – величина z в децибелах, равная 20*LOG(|z|); RE(z) – действительная часть z; IM(z) – мнимая часть z; MAG(z) – модуль z.
При построении графиков допустимо просто указать z; PH(z) – фаза z в градусах; GD(z) – групповое время запаздывания. Операции с логическими переменными см. в [3,4].
Операторы обработки сигналов при построении графиков:
HARM(u) – расчет гармоник сигнала u; THD(S) – коэффициент нелинейных искажений спектра S, в процентах относительно уровня первой гармоники; FFT(u) – прямое преобразование Фурье дискретных отсчетов сигнала u(t). Отличается от функции HARM множителем N/2 для гармоник с первой до N-й и множителем N для нулевой гармоники, где N – количество дискретных отсчетов сигнала u(t); IFT(S) – обратное преобразование Фурье спектра S; CONJ(S) – сопряженный комплексный спектр S; CS(S, S2) – взаимный спектр сигналов u и v, равный CONJ(FFT(S)*FFT(S2)); AS(S) – cобственный спектр сигнала u(t), равный CS(S, S); CC(u,v) – взаимная корреляционная функция сигналов u и v, равная IFT(CS(u, v)); AC(u) –автокорреляционная функция сигнала u, равная IFT(AS(u)); COH(u,v) – нормированная корреляционная функция сигналов u и v, равная CC(u,v)/SQR(AC(u(0))*AC(v(0))); REAL(S) – действительная часть спектра S, рассчитанного с помощью FFT; IMAG(S) – мнимая часть спектра S, рассчитанного с помощью FFT; MAG(S) – модуль спектра S, рассчитанного с помощью FFT; PHASE(S) – фаза спектра S, рассчитанного с помощью FFT.
Моделей ОУ в ССМ МСV.
Цель работы: изучить возможности моделирования схем сложных операционных усилителей (ОУ) в ССМ МСV.2; ознакомиться с частотными и переходными характеристиками ОУ; познакомиться с влиянием параметров 3х основных математических моделей ОУ на их частотные и переходные характеристики.
Моделирование фильтра на отрезках линии передачи
Второй пример иллюстрирует использование линии задержки как Z задерживающего звена при моделировании цифрового фильтра [11]. В этом примере демонстрируется использование идеальной линии передачи без потерь для моделирования рекурсивного цифрового фильтра [7.2] Баттерворта третьего порядка. Системная функция такого фильтра имеет вид:
H (z) = (0.156z-1 + 0.183z-2)/(1- 1. 081z-1 + 0.607z-2 - 0.123z-3) (6.1)
Структурная схема фильтра, соответствующая (6.1), показана на Рис. 6.8 [11]. С использованием линий передачи и структурных схем фильтров, пред-ставляемых на их основе, моделирование цифровых фильтров становится более простым и наглядным, чем использование системных функций и зависимых источников, задаваемых Z – преобразованием, особенно в учебном процессе.

Рис. 6.8
Принципиальная схема фильтра, соответствующая Рис. 6.8, показана на Рис. 6.9. Отрезок идеальной линии передачи на Рис. 6.9 соответствует элементу z-1 на Рис. 6.8 и в системной функции (6.1) фильтра. Линия задержки определяется волновым сопротивлением Z0 и временем задержки TD. Значение волно-вого сопротивления роли не играет, пока линия нагружена на сопротивление, равное волновому. Параметр задержки TD определяет интервал осуществления выборки сигнала в ЦФ или частоту дискретизации FC. Источники на входе отрезков линии передачи – это зависимые ИНУН (см. п. 3.1) с коэффициентом передачи, равным 1. Эти источники играют роль буферов, разделяющих после-довательно включённые элементы задержки.

Рис. 6.9
На вход фильтра включён такой же источник V1, как и на вход фильтра первого примера (см. Рис. 6.1 и Рис. 6.2). Два сумматора структурной схемы Рис. 6.8 выполнены на нелинейных зависимых источниках напряжения, управлямых напряжением (см. п. 3.2 и Рис. 3.7). Для правильного сумми-рования сигналов в соответствии с Рис. 6.8 нужно правильно определить атрибуты этих источников. Окно атрибутов источника SUM1 показано на Рис. 6.10, а источника SUM2 – на Рис. 6.11.

Рис. 6.10

Рис. 6.11
На Рис. 6.12 приведено окно пределов анализа фильтра во временной области, а на Рис. 6.13 – результаты этого анализа. В форме выходного сигнала на Рис. 6.13 характерно выделяются перепады напряжения на интервалах времени, длительностью 50 мс.
На Рис. 6.14 приведено окно пределов анализа фильтра в частотной области, а на Рис. 6.15 – результаты расчёта АЧХ рассматриваемого фильтра.
Из Рис. 6.15 виден очень характерный для фильтров этого типа момент – периодическое повторение АЧХ фильтра через 20 кГц, которое соответствуют частоте дискретизации фильтра.

Рис. 6.12
Принципиальная схема фильтра, соответствующая Рис. 6.8, показана на Рис. 6.9. Отрезок идеальной линии передачи на Рис. 6.9 соответствует элементу z-1 на Рис. 6.8 и в системной функции (6.1) фильтра. Линия задержки определяется волновым сопротивлением Z0 и временем задержки TD. Значение волно-вого сопротивления роли не играет, пока линия нагружена на сопротивление, равное волновому. Параметр задержки TD определяет интервал осуществления выборки сигнала в ЦФ или частоту дискретизации FC. Источники на входе отрезков линии передачи – это зависимые ИНУН (см. п. 3.1) с коэффициентом передачи, равным 1. Эти источники играют роль буферов, разделяющих после-довательно включённые элементы задержки.

Моделирование фильтра на переключаемых конденсаторах
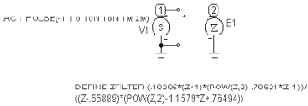
H (z) = (0.10285 (z + 1) (z2 -0. 70621z + 1)) / (z-0. 55889 )( z2 -1. 1579z + 0.76494)
В первом примере для моделирования фильтра используются два источника сигналов, как это показано на Рис.6.1.
Схема содержит лишь два компонента. Первый-независимый источник напряжения V (см. п. 3 пособия), который обеспечивает входное воздействие.
Рис. 6.1 Источник V для анализа переходных процессов на выходе фильтра определен в окне атрибутов как источник импульсов с амплитудой импульсов +/-1в, длительностью импульсов 1мс, временем нарастания импульсов 10нс, временем спада импульсов 10нс и периодом повторения импульсов 2мс (см. Рис. 6.2). Для анализа АЧХ фильтра источник напряжения V определён как источник синусоидального сигнала амплитудой в 1В.

Рис. 6.2
Второй источник – линейный зависимый источник Е1, задаваемый Z – преоб-разованием, который является электрическим эквивалентом фильтра с переключаемыми конденсаторами и определяется указанной выше системной функцией фильтра в z плоскости (см. Рис. 6.3).

Рис. 6.3
На Рис. 6.4 приведено окно пределов анализа фильтра во временной области, а на Рис. 6.5 – результаты анализа. Анализ переходных процессов наглядно показывает интервал осуществления выборки 41,6 мс и степень искажения формы импульса (см. фронты импульсов).

Рис. 6.4
Copyright © 2000 Георгий Долин. All rights reserved. Design - "Kety studio" by Alex Kazantsev. Support - "Anri Education Systems"

Рис. 6.5
На Рис. 6.6 приведено окно пределов анализа фильтра в частотной области, а на Рис. 6.7 – результаты расчёта АЧХ фильтра. Технические данные этого фильтра: граничная частота – 3,2 кГц, уровень искажений на граничной частоте - 0.9 дБ, уровень ослабления на частоте 4,3 кГц больше или равен 22 дБ [7.2]. Результаты анализа показывают, что АЧХ фильтра соответствуют этим данным.

Рис. 6.6

Рис. 6.7
Нелинейные зависимые источники электрических сигналов
В MC5 имеются четыре нелинейных зависимых источника с полиномиальным законом управления. Путь к источникам: Component и Analog Primitives и Dependent Sources. Подробнее рассмотрим их особенности на примере источника тока, управляемого напряжением.

Рис.3.5. УГО POLY ИТУН
y= P0 + P1x1 + P2x2 +…+ Pkxk + Pk+1x12 + Pk+2x1x2 +…+ Pk+kx1xk+ P2k+1x22 + P2k+2x2x3 +…+ P2k+kx2x3 + … (3.1)
При конкретной записи полинома все коэффициенты вводить не нужно, но те, что вводятся, должны следовать строго по порядку. Параметры рассматриваемых источников также целесообразно вводить в схему используя окно атрибутов (но можно и текстовой директивой). Атрибут PART (см. [10]) имеет обычное буквенно-цифровое обозначение, например, I1. Атрибут VALUE для ИТУНа имеет следующую форму записи:
POLY (K) n1p n1m [n2p n2m] … [nkp nkm] [P0 P1 … PK] [IC=C1[, C2[, … CK]]] (3.2)
Здесь: K –число управляющих напряжений,
n1p – положительный полюс 1го управляющего напряжения,
n1m – отрицательный полюс 1го управляющего напряжения,
nkp – положительный полюс kго управляющего напряжения,
nkm – отрицательный полюс kго управляющего напряжения,
P0 … Pk – коэффициенты полинома,
C1, C2, …, Ck – начальные условия (используются редко).
Рассмотрим несколько примеров использования ИТУНа (GIofV) для иллюстрации возможностей рассматриваемых источников.
Линейная модель ЭЛ или БТ. Ток источника связан с управляющим напряжением следующим соотношением: I=SUупр.Пусть одно управляющее напряжение действует между узлами 3 и 0, т.е. Uупр = U (3,0). Полином (3.1) в данном случае имеет вид: y=P0+P1x1 = 0 + S*U(3,0) = 0 +0.1*V(3,0). Отсюда атрибуты источника следует представлять в виде: PART=G1 (см. Рис. 3.5 ); VALUE = POLY(1) 3 0 0.0 0.1 При вводе этого источника текстовой директивой запись ее выглядит следующим образом: . define G1 POLY(1) 3 0 0.0 0.1
Нелинейная модель полевого транзистора. Ток источника в этом случае связан с управляющим напряжением следующим образом: I=SUупр2. Пусть одно управляющее напряжение действует между узлами 6 и 5. Полином (3.1) в данном случае имеет вид y= P0 + P1x1 + P2x12 = 0 + 0*x1 + S*V(6,5)*V(6,5) = 0+ 0*V(6,5)+0.01*V(6,5)*V(6,5). Отсюда атрибуты источника GIofV нужно представить в виде: PART=G1 (см. Рис. 3.5); VALUE = POLY(1) 6 5 0.0 0.0 0.01
Пример использования источника GIofV в качестве сумматора воздействия нескольких переменных приведен в пункте 6 настоящего пособия.

Рис.3.6. УГО POLY ИТУТ
2. Источник тока, управляемый током (ИТУТ). УГО этого источника приведено на Рис 3.6. Имя источника в библиотеке пассивных компонентов имеет вид FIofI. Атрибут PART источника имеет обычное буквенно-цифровое обозначение, например I3. Атрибут VALUE имеет следующую форму записи:
POLY(K) V1 [V2…VK] P0 [P1 … PK] [IC=C1[, C2[, … CK]]], (3.3)
где V1 – имя (см. п. 4) 1-го независимого источника напряжения, ток которого служит первым управляющим током, VK-имя Кго независимого источника напряжения, ток которого служит Кым управляющим током. Остальные коэффициенты и параметры полинома были определены выше в подпункте 1.
Выполним на базе источника FIofI перемножитель двух переменных (токов) вида y=kx1x2. Полином (3.1) в этом случае имеет вид:
y= P0+P1x1+ P2x2 + P3x12+P4x1x2 +P5x22 = 0+0x1+ 0x2 + 0x12+Кx1x2 +0x22
Атрибуты источника-перемножителя двух переменных при К=12 будут равны:
PART=I3 (см. рис. 3.6); VALUE=POLY(2) V1 V2 0.0 0.0 0.0 0.0 12.0
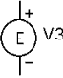
УГО источника напряжения приведено на Рис. 3.7. Имя источника в библиотеке пассивных компонентов имеет вид EVofV. Атрибут PART источника имеет обычное обозначение, например, V3. Атрибут VALUE имеет форму записи, соответствующую (3.2). Выразим на базе источника EVofV простейшую модель ОУ с коэффициентом усиления K=100000.
Рис.3.7. УГО POLY ИНУН
Соотношение между управляющим Vупр и выходным Vвых напряжениями источника равно: Vвых = КVвх, т.е. источник управляется только одной переменной. Полином (3.1) имеет вид y=P0+P1x1. Пусть управляющее напряжение действует между узлами 3 и 4. Тогда атрибуты источника равны:
PART = V3 (см. Рис 3.7);
VALUE = POLY(1) 3 4 0.0 100Е3

Рис.3.8. УГО POLY ИНУТ



Независимые источники напряжения и тока
Независимые источники напряжения с именем V и независимые источники тока с именем I в библиотеке компонентов используются при всех видах анализа схем, включая режим Stepping [4]. Путь к их именам тот же, что и для синусоидального источника напряжения. УГО источника напряжения приведено на Рис 4.7, а УГО источника тока – на Рис. 4.8.
 Рис. 4.1 |
 Рис. 4.2 |
Рассматриваемые независимые источники позволяют моделировать воздействие на схему сигналов самой разнообразной формы напряжения или тока: постоянного напряжения или тока, синусоидальные с заданной амплитудой и/или начальной фазой, импульсные, экспоненциальные, их сочетание, кусочно-линейные и с частотной модуляцией. Вводить параметры этих источников также целесообразно с использованием окна атрибутов. Атрибутов два: PART=V4, VALUE= «список параметров источника». Параметры этих источников задаются в формате программы PSpice [3]. Формат параметров следующий: VALUE=[DC P0] [AC P1 [P2]] [параметры выбранного истоника сигнала]. Здесь P0 – величина постоянной составляющей напряжения или тока; P1 – амплитуда; P2 – начальная фаза синусоидального сигнала. Параметрами выбранного источника могут быть:

Импульсный сигнал PULSE имеет параметры [4], пояснения к которым приведены в Таб. 4.1. Таб.4.1

Синусоидальный сигнал SIN имеет параметры [4], пояснения к которым приведены в Таб. 4.2.

Параметры экспоненциального сигнала EXP можно найти в [3,4].
Синусоидальная функция с частотной модуляцией SFFM определяется выражением y(t) = y0 + ya sin[2 p freq t + mi sin(2 p fm t)]. Параметры этой функции приведены в Таб. 4.3.

Кусочно – линейный сигнал в учебном процессе используется редко и здесь его параметры не приводятся, но их можно найти в [4].
Рассмотрим примеры представления параметров источников V и I.
Источник постоянного напряжения и синусоидального напряжения аплитудой 1 В и нулевой начальной фазой.
PART=V1
VALUE=DC 0.5 AC 1V
Источник импульсного тока.
PART = I4;
VALUE = PULSE 1.0 3.0 1N 1N 2N 50N 0.2
Синусоидальный источник напряжения
PART = V6;
VALUE = SIN 0.0 0.1 10K
Большое число примеров использования источников V и I приведено в
[3,6,10].
Общие положения
При анализе и синтезе дискретных и цифровых устройств широко используется Z – преобразование, играющее по отношению к дискретным сигналам такую же роль, как преобразования Фурье и Лапласа по отношению к непрерывным сигналам [11]. Весьма широко и конструктивно с использовани-ем Z – преобразования проводится синтез цифровых фильтров, а реализация их осуществляется и программно [12]. Использование ПЭВМ и ССМ, содержащих аппарат преобразования Лапласа, например, МС5, позволяет проводить машинное моделирование дискретных систем типа фильтров с переключаемыми конденсаторами и цифровых фильтров на отрезках длинных линий. Важность этого момента для учебных целей очевидна.
В формате SPICE нет источника, реализующего Z преобразование. Поэтому в MC5 версии 2 вводится собственный формат для линейных зависимых источников, задаваемых Z – преобразованием с использованием выражения от комплексной переменной Z. Описание этих источников было приведено в п. 3.5 пособия.
Z - преобразование задается следующим уравнением:

где: z-n - оператор задержки, n - число единичных задержек, T - интервал осуществления выборки и V(nT) - дискретные аналоговые выборки. Это уравнение не может быть вычислено непосредственно в MC5. Но в MC5 можно провести эквивалентное преобразование по Лапласу. С использованием источника, задаваемого преобразованием Лапласа, любые функции Z - преобразования могут быть переведены в функции преобразования по Лапласу через замену: Z = e sT. Но в МС5 пользователь работает непосредственно с выражениями от переменной z. Рассмотрим два основных примера.
Окно редактора и меню редактора электрических схем




Copyright © 2000 Георгий Долин. All rights reserved. Design - "Kety studio" by Alex Kazantsev. Support - "Anri Education Systems"
Панели инструментов редактирования схем и проведения анализа
Инструментальная панель представленная на рис. 2.1. используется для быстрого и наглядного выполнения команд. Она используется как при вводе и редактировании схемы, так и при проведении анализа.
Диалоговое окно ToolBar позволяет определять какие кнопки и соответствующие им команды будут доступны в инструментальной панели.

В поле левого окна представлен список групп сформированных кнопок. Все кнопки, за исключением кнопок группы Component, фиксированы, неизменяемы. Их можно либо помещать на Панели инструментов, либо нет. Для этого следует либо включать переключатели Schematic и Analysis в окне Tool Bar (щелчок мыши в поле переключателя до появления «галочки»), либо выключать их (щелчком мыши в поле переключателя). Переключатель Schematic определяет появление кнопок на Панели инструментов в режиме ввода схем, переключатель Analysis – в режиме анализа схем.
Кнопки группы Component (см. рис. ниже) позволяют обеспечить быстрый выбор компонентов при вводе и редактировании электрических схем. Щелчок по кнопке во втором поле вызывает появление рисунка, находящегося на кнопке соответствующего компонента. С помощью щелчков мыши можно изменять рису нок выбранной кнопки в правом поле. Ниже этого поля расположено окно с именем компонента. Используя кнопку Browse (Поиск) можно просмотреть имена компонентов, представленных кнопками.

Для добавления новой кнопки в группу Component следует выбрать одну из пустых кнопок, ввести стандартное имя компонента, создать условный рисунок компонента и нажать клавишу OK. Назначение клавиш в диалоговом окне Tool Bar приведено ниже.

Цель работы
Цель работы: познакомиться с методикой составления и редактирования принципиальных схем РТУ; изучить способы использования математических моделей БТ для моделирования РТУ; практически освоить особенности анализа принципиальной схемы РТУ и оценку результатов её анализа, особенно проверку режимов работы УЭ по постоянному току; ознакомиться с основными характеристиками КПУ и сопоставить их с характеристиками КПУ, полученными на базе эквивалентных схем (2 и 3 занятия).
Создание новой библиотеки
Программа МС5.2 поставляется с большой библиотекой компонентов (библиотека профессиональной версии содержит около 10 тыс. компонентов). Однако возникает необходимость ее пополнения, в первую очередь за счет создания библиотеки отечественных компонентов и макромоделей типовых устройств. Студенческая версия МС5.2 также требует пополнения библиотеки компонентов, ещё лучше – создания новой, подходящей для учебных целей.

Создание новой библиотеки начинается с вызова диалогового окна New (Рис. 2.1.) командой File->New из меню главного окна. В появившемся диалоговом окне выбираем создание библиотеки (Library-Рис.2.1). После чего открывается диалоговое окно (Рис. 2.2.), которое позволяет создавать и редактировать компоненты в новой библиотеке. Если требуется сохранить новую библиотеку, то по команде File->Save открывается диалоговое окно (Рис. 2.3.). Если в процессе работы с MC5 требуется открыть ранее сделанную библиотеку или библиотеку, входящую в состав поставки MC5, то по команде меню File->Open открывается диалоговое окно (Рис. 2.4.). В нижнем поле окна выбираем для открытия файлы библиотеки, т.е. Model Library [*.LBR]. В левом верхнем поле в открывшемся списке выбираем имя требуемой библиотеки.
Новую библиотеку можно подключить к системе MC5 несколькими способами:
Если компоненты из библиотеки используются только в одной схеме, то имя файла библиотеки можно указать с помощью атрибута символа компонента FILE, например FILE= OP.LIB; В файле, имя которого непосредственно указывается с помощью директивы .LIB, например .LIB OP.LIB; В файле, ссылка на который (например .LIB OP.LIB) помещается в файл NOM.LIB, загружаемый в программу МС5 по умолчанию по директиве .LIB NOM.LIB (этот способ наиболее удобен для отлаженных библиотек).


Рис.2.5. Добавление нового компонента в библиотеку компонентов



Copyright © 2000 Георгий Долин. All rights reserved. Design - "Kety studio" by Alex Kazantsev. Support - "Anri Education Systems"
Установка и запуск системы схемотехнического моделирования МСV
Демонстрационная (студенческая) версия содержится в .ZIP файле (ее можно скачать с сервера фирмы Spectrum Software - http://www.spectrum- soft.com). После раскрытия этого файла программой PKUNZIP запустите программу SETUP.EXE под Windows 3.X, Windows NT или Windows 95. В ходе установки программы она запросит Диск 2. Когда эта подсказка появится, нажмите <Enter> при проведении установки с жесткого диска. Если проводится установка с гибких дисков, то она продолжится после установки в дисковод Диска 2. После завершения установки в указанном каталоге оказываются 10 файлов и образуется папка Micro-CAPV Working Demo для быстрого запуска МСV. В подкаталог МСVdemo\data заносятся файлы схем, имеющие расширение имени .CIR, и библиотеки математических моделей компонентов в файлах с расширением .LBR.
Запуск программы. Студенческая версия программы MCV запускается на выполнение командой: MCVDEMO.EXE
При указании за командой имени файла загружается указанная схема: причем, если указано имя файла без расширения имени, то загружается файл с расширением имени .cir
Обратим внимание: в подкаталоге \DATA размещаются файлы пользователей, имеющие произвольные имена и стандартные расширения, имеющие следующий смысл:

Задание на «хорошо»
7. Собрать представленные на Рис.3 схемы с LFVofV.
|
|
|
8. Получить ФЧХ для схем Рис.3, оценить и записать yв для fср.в.
9. Получить переходные процессы для схем Рис.3 и зарисовать их. Записать Uвх, Uвых, tуст.
10. Сделать выводы о совпадении АЧХ, ФЧХ и ПХ интегрирующих и дифференцирующих цепочек первого и второго занятий.
4.Получить зависимость Zвхтр = F(f), где Zвхтр = Uвх/Iвх = V(3,0)/I(rb).
5. Получить зависимость Rвхтр = F(f), где Rвхтр = Uвх/Iвх = Re[V(3,0)/I(rb)].
Записать значения Rвхтр для fнч, fср и fвч. Зафиксировать различия между Zвхтр и Rвхтр .
6. Получить зависимость Bвхтр = F(f), где Bвхтр = Im[I(rb) / V(3,0)].
3. Получить зависимость Rвхтр=F(f),где: Rвхус=Uвх/Iвх=Re(V(3,0) / Ib(Q2N2511)) .
Записать значение Rвхтр для fнч , fср и fвч.
4. Получить зависимость Bвхтр = F(f), где: Bвхтр= Im[Ib(Q2N2511) / V(3,0)].
Записать значения Bвхтр для fнч , fср и fвч.
5. Сравнить Rвхтр и Bвхтр, полученные на 3, 4 и 5 занятиях.
5. Подключить ко входу ОУей источник импульсного сигнала.
6. Получить переходный процесс на выходе всех трёх моделей ОУ (на одном графике). Пределы анализа уже установлены в учебном файле.
7. Зарисовать от руки примерную форму импульсов на выходе всех ОУ. Пояснить отличия в виде переходных процессов (изменение формы импульсов) на выходе всех 3х ОУ.
8. Увеличить в 2-4 раза длительность импульсов на входе ОУ и повторить пункты 5-7 задания. Объяснить изменения в форме импульсов на выходе ОУ.
3. Получить переходный процесс при большом синусоидальном сигнале на входе (Umвх » 0.7*Епит). Оценить для схем 1-4 Uвыхmax по нелинейным искажениям сигнала на средних частотах 1-3 кГц для Кг = 3%.
Задание на «отлично»
12. Установить форму импульсного сигнала на входе RC цепочек, соответствующую получению их импульсной характеристики (см. книгу Разевига по МСV).
13. Получить импульсную характеристику интегрирующей и дифференцирующей цепочек и зарисовать их ( качественно).
14. Установить форму импульсного сигнала на входе RC цепочек, соответствующую получению переходной характеристики ( см. книгу Разевига по МСV).
15. Получить переходную характеристику обеих цепочек и зарисовать их ( качественно).



Copyright © 2000 Георгий Долин. All rights reserved. Design - "Kety studio" by Alex Kazantsev. Support - "Anri Education Systems"
11. Собрать представленные на рис.4 схемы.
|
|
|
13. Установить в схемах рис.4 сопротивление нагрузки R1=100 Ом. Получить АЧХ в виде зависимости Y(f), а не Uвых(f) или Ku(f), где Y(f) = Ku(f)/Ku(fсред) = Uвых(f)/Uвых(fср).





