Анализ адекватности ассоциативных сетей
Основную операцию извлечения информации в той модели обработки, которая следует из предложенной Квиллианом модели памяти, можно охарактеризовать как распространяющуюся активность. Идея состоит в том, что если желательно знать, является ли телетайп машиной, то необходимо искать, т.е. распространить "активность" некоторого вида во всех направлениях — как от узла-типа " телетайп", так и от узла-типа "машина". Если где-то эти две волны встретятся, то таким образом будет установлено существование связи между этими двумя концептами, т.е. определен путь на графе от одного узла к другому. Такая распространяющаяся в разных направлениях активность реализуется передачей маркеров вдоль именованных связей. Мы еще раз вернемся к этой, на первый взгляд, простой, но довольно продуктивной идее при обсуждении нейронных сетей в главе 23.
Интересно отметить, что идеи Квиллиана не получили широкого распространения в качестве модели психологической организации и функционирования памяти человека. При проверке адекватности этой модели Коллинс и Квиллиан измеряли время, которое требовалось испытуемым для ответа на вопрос о принадлежности определенного понятия к некоторой категории и о его свойствах [Collins and Quillian, 1969]. Оказалось, что время, затрачиваемое на поиск ответа, действительно увеличивается по мере увеличения количества узлов в сети, описывающей связи между понятиями. Однако такая зависимость имела место только в отношении положительных ответов. Существовали определенные подозрения, что применение предложенной модели для случая отрицательных ответов натолкнется на определенные трудности. И последующие эксперименты, проведенные другими исследователями, эти подозрения подтвердили.
Тем не менее Квиллиан продолжал исследование возможности использования формализма сетей для представления знаний. Хотя современное представление об ассоциативных сетях во многом существенно отличается от первоначальной концепции и область их использования включает множество проблем, отличных от понимания смысла предложений естественного языка, многие базовые принципы унаследованы от пионерских работ Квиллиана, упомянутых выше.
Существует довольно обширный перечень проблем, при решении которых представление, базирующееся на формализме ассоциативных сетей, оказывается весьма полезным. В 1970-х годах было опубликовано множество работ, в которых анализировались различные виды такого формализма. Наиболее удачной из них, на наш взгляд, является работа Вудса [Woods, 1975]. Использование узлов и связей в сети для представления понятий и отношений между ними может показаться само собой разумеющимся, но опыт показал, что на этом пути неосторожного путника поджидает множество ловушек.
В различных вариантах спецификаций структуры сети далеко не всегда четко определяется смысл маркировки узлов. Так, если рассмотреть узел-тип, имеющий маркировку "телетайп", то часто бывает непонятно, представляет ли этот узел понятие "телетайп", или класс всех агрегатов типа "телетайп", или какой-либо конкретный телетайп. Аналогично, и узел-лексема также открыт для множества толкований — определенный телетайп, какой-то телетайп, произвольные телетайпы и т.д. Разные толкования влекут за собой и разный характер влияния этого узла на другие в сети, а это играет весьма важную роль в дальнейшем анализе.
Поиск пересечения неизбежно "тянет за собой" проблему преодоления комбинаторного взрыва, о которой шла речь в главе 2. Поэтому создается впечатление, что организация памяти в терминах множества узлов, для которых в качестве главного вида процесса извлечения используется распространяющаяся по всем направлениям активность, приведет к образованию системы с труднопредсказуемым поведением. Например, весьма вероятно, что при отрицательных ответах на запросы придется выполнить огромное количество элементарных действий, поскольку нужно убедиться, что не существует пересекающихся путей на графе сети между двумя заданными узлами.
Из сказанного выше ясно, что первоначальные виды формализмов ассоциативных сетей страдают минимум двумя недостатками.
Сети являются логически неадекватными, поскольку в них нельзя представить множество различий, представимых в логическом исчислении, например различие между определенным телетайпом, любым единственным телетайпом, всеми телетайпами, ни одним телетайпом и т.д.
Смысл или значение, которые ассоциируются с узлами и связями в сети, часто сложным образом связаны с такими характеристиками системы, как способность к извлечению информации и анализу взаимовлияний. Такое смешение семантики с деталями реализации является результатом того, что сети одновременно являются и средством представления знаний, и средством извлечения из них нужной информации, и средством конструирования заключений, основанных на знаниях, причем везде используется один и тот же набор ассоциативных механизмов. Естественно, что при этом различия между тремя означенными сторонами модели представления смазываются, теряют четкость.
Сети являются эвристически неадекватными, поскольку поиск информации в ней сам по себе знаниями не управляется. Другими словами, этот механизм не предполагает наличия какого-либо знания о том, как искать нужную нам информацию в представленных знаниях. Эти два недостатка иногда "усиливают" друг друга самым неприятным образом. Например, если невозможно представить логическое отрицание или исключение (логическая неадекватность), это приведет к определенным "провалам" в знаниях, которые к тому же нельзя ликвидировать эвристически, прекратив поиск в этом направлении (эвристическая неадекватность).
Для разрешения описанных проблем предлагались самые разные формализмы и механизмы, но лишь немногие из них нашли широкое распространение. Например, многие системы, базирующиеся на сетевом представлении, были расширены и в результате получили множество свойств, характерных для чисто логических систем (см., например, [Schubert, 1976]). В других системах эвристики использовались таким образом, что с каждым узлом связывались процедуры, которые выполнялись, как только узел активизировался (см., например, [Levesque and Mylopoulos, 1979]). Как бы там ни было, но основной принцип организации памяти в терминах узлов и связей остается прежним, несмотря на использование всякого рода дополнительных структур, например "суперузлов" [Hendrix, 1979]. Образующиеся в результате системы часто плохо контролируются пользователем и, утрачивая при этом первоначальную простоту, мало что приобретают в смысле функциональных характеристик.
Ассоциативные сети
Систематические исследования методики использования сетей для представления знаний начались с исследования методов представления семантики естественного языка [Quillian, 1968]. Квиллиан предположил, что наша способность понимать язык может быть охарактеризована, хотя бы в принципе, некоторым множеством правил. Он предположил, что процесс восприятия текста включает в себя "создание некоторого рода мысленного символического представления". Исходя из этого, он занялся изучением вопроса, как смысл отдельных слов может быть сохранен в компьютере, чтобы компьютер смог использовать их по тому же принципу, что и человек. Квиллиан был не первым, кто обратил внимание на важность обобщенного, абстрактного знания для понимания естественного языка. Еще ранее к такому же заключению пришли исследователи, занимавшиеся проблемами машинного перевода. Но Квиллиан первым предложил использовать для моделирования человеческой памяти сетевые структуры, в которых узлы и связи между ними представляли бы концепты и отношения между концептами. Он же предложил работающую модель извлечения информации из памяти.
Если мы стремимся создать программу, устойчивую к модификации данных, т.е. сохраняющую работоспособность при множестве таких модификаций, то нам непременно понадобится какое-либо средство проверки целостности знаний. Это, в свою очередь, накладывает определенные ограничения на методы представления знаний: знания должны быть организованы таким образом, чтобы упростить проверку их целостности. Именно такая цель преследовалась при создании тех видов структуры представления знаний, которые мы будем рассматривать в этой главе.
Ассоциативные сети и системы фреймов
6.1. Графы, деревья и сети
6.2. Ассоциативные сети
6.3. Представление типовых объектов и ситуаций
Рекомендуемая литература
Упражнения
Следуя Нильсону [Nilsson, 1982], я буду использовать термин структурированный объект по отношению к любой схеме представления, базовые блоки которой аналогичны узлам и дугам в теории графов или слотам и заполнителям структур записей. Я буду систематически сравнивать этот вид представления со схемами, производными от правил формальных грамматик или формализмов разнообразных логик. Представление с помощью структурированных объектов является весьма удобным средством для группирования информации более или менее естественным путем.
В предыдущей главе уже отмечалось, что порождающие правила очень подходят для представления связей состояния некоторой проблемы с действиями, которые необходимо предпринять для продвижения к искомому решению. Однако иногда для решения проблемы больший интерес представляет не ответ на вопрос "Что делать, если...?", а свойства и взаимоотношения между сложными объектами в предметной области. Представлять знания о таких объектах и событиях и их взаимосвязях (таких как тип — подтип, часть — целое, до — после и т.д.) с помощью формальных правил далеко не всегда удобно.
В этой и следующей главах мы рассмотрим способы, удобные для представления структурированных знаний, и остановимся на тех трудностях, с которыми столкнулись исследователи на практике. Формальный аппарат, который будет использован в данной главе, базируется на различных видах графов, узлы которых хранят информацию о сущностях в форме записей, а дуги определяют взаимоотношения между этими сущностями. В следующей главе мы рассмотрим объектно-ориентированный подход к представлению знаний, который влечет за собой определенную методологию разработки и соответствующий стиль программирования.
Фреймы и графы
Минский в свой работе [Minsky, 1975] определил фрейм как "структуру данных для представления стереотипных ситуаций". Эту структуру он наполнил самой разнообразной информацией: об объектах и событиях, которые следует ожидать в этой" ситуации, и о том, как использовать информацию, имеющуюся во фрейме. Идея состояла в том, чтобы сконцентрировать все знания о данном классе объектов или событий в единой структуре данных, а не распределять их между множеством более мелких структур вроде логических формул или порождающих правил. Такие знания либо сосредоточены в самой структуре данных, либо доступны из этой структуры (например, хранятся в другой структуре, связанной с фреймом).
Таким образом, по существу, фрейм оказался тем средством, которое помогло связать декларативные и процедурные знания о некоторой сущности в структуру записей, которая состоит из слотов и наполнителей (filler). Слоты играют ту же роль, что и поля в записи, а наполнители — это значения, хранящиеся в полях. Однако, как будет сказано ниже, фреймы отличаются от привычных программных структур вроде записей в языке PASCAL.
Каждый фрейм имеет специальный слот, заполненный наименованием сущности, которую он представляет. Другие слоты заполнены значениями разнообразных атрибутов, ассоциирующихся с объектом. Это могут быть и процедуры, которые необходимо активизировать всякий раз, когда осуществляется доступ к фрейму или его обновление. Идея состоит в том, чтобы выполнение большей части вычислений, связанных с решением проблемы, явилось побочным эффектом передачи данных во фрейм или извлечения данных из него.
Фрейм также можно рассматривать как сложный узел в особого вида ассоциативной сети. Как правило, фреймы организованы в виде "ослабленной иерархии" (или "гетерархии"), в которой фреймы, расположенные ниже в сети, могут наследовать значения слотов разных фреймов, расположенных выше. (Гетерархия — это "запутанная иерархия", т.е. ациклический граф, в котором узлы могут иметь более одного предшественника.)
Фундаментальная идея состоит в том, что свойства и процедуры, ассоциированные с фреймами в виде свойств узлов, расположенных выше в системе фреймов, являются более или менее фиксированными, поскольку они представляют те вещи или понятия, которые в большинстве случаев являются истинными для интересующей нас сущности, в то время как фреймы более нижних уровней имеют слоты, которые должны быть заполнены наиболее динамической информацией, подверженной частым изменениям. Если такого рода динамическая информация отсутствует из-за неполноты наших знаний о наиболее вероятном состоянии дел, то слоты фреймов более нижних уровней заполняются данными, унаследованными от фреймов более верхних уровней, которые носят глобальный характер. Данные, которые передаются в процессе функционирования системы от посторонних источников знаний во фреймы нижних уровней, имеют более высокий приоритет, чем данные, унаследованные от фреймов более верхних уровней.
Среди связей в системе фреймов особо нужно выделить связи между экземплярами и классами и связи между классами и суперклассами. Узел Компьютер имеет связь с узлом Машина, которая представляет отношение "класс-суперкласс", а узел sol2, представляющий конкретный компьютер (тот, на котором я работаю), имеет связь с узлом Компьютер, которая представляет отношение "экземпляр-класс". Свойства и отношения, которые в типичной семантической сети кодируются маркировкой связей между узлами, теперь кодируются с помощью представления слот-заполнитель. Кроме того, со слотами может быть ассоциирована любая дополнительная информация, например процедуры вычисления значения этого слота в случае отсутствия явного его заполнения, процедуры обновления значения слота при изменении значения другого слота, ограничения на величины, хранящиеся в слотах, и т.д.
Графы, деревья и сети
Для описания многих видов абстрактных данных в информатике вообще и в теории искусственного интеллекта, в частности, очень широко используется терминология, заимствованная из теории графов. Следующие определения приведены здесь для того, чтобы показать, как эти заимствованные термины трактуются при описании структурированных объектов, что несколько отличается от их трактовки в "родной" математической сфере.
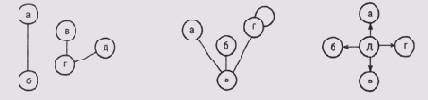
Рис. 6.1. Некоторые виды графов: а) обыкновенный граф; б) связный граф с петлей; в) обыкновенный ориентированный граф — дерево
Все определения сформулированы в предположении, что существуют два вида примитивов — узлы и связи. Узлы представляют собой исходящие и целевые пункты для связей и обычно каким-либо образом промаркированы. Связи также могут быть промаркированы, но это не обязательно. Все зависит от того, имеем ли мы дело со связями одного вида или разных. В общепринятой терминологии теории графов узлы называются "вершинами", а связи — "ребрами графа", или "дугами".
Определение 6.1. Если N— множество узлов, то любое подмножество NxN является обобщенным графом G. Если в парах подмножества NxN имеет значение порядок, то граф G является ориентированным.
На рис. 6.1 показаны разные типы графов. Обратите внимание на то, что граф не обязательно должен быть связным. Если задаться условием, что петли не допускаются, т.е. в каждой паре должны присутствовать разные узлы, то такой граф называется обыкновенным. Если на графе не допускаются не только петли, но и циклы (т.е. последовательность связей, в которой начальный и конечный узлы совпадают), то такой граф называется лесом.
Определение 6.2. Если G— обыкновенный граф, в котором имеется п узлов и п-1 связей и отсутствуют циклы, то такой граф является деревом.
Иными словами, дерево — это связный лес. Обычно один из узлов дерева является его корнем, например узел е на графе, представленном на рис. 6.1,в. Остальные узлы образуют ветвящуюся структуру "наследников" корневого узла, в которой отсутствуют циклы.
Узлы, не имеющие наследников, являются терминальными, или "листьями" дерева, а остальные узлы называются промежуточными (нетерминальными).
В теории графов сетью называется взвешенный ориентированный граф, т.е. граф, в котором каждой связи сопоставлено определенное число. Обычно этими числами оценивается "стоимость" пути вдоль этой связи или длина связи, как на карте дорог. В каждом конкретном случае применения графа как формального средства описания проблемы эти числа могут трактоваться по-своему.
Следующее определение сети более близко к специфике задач искусственного интеллекта, которыми мы сейчас занимаемся.
Определение 6.3. Если L — это множество взвешенных связей, a N, как и ранее, множество узлов, то сеть — это любое подмножество NxLxN, в котором имеет значение порядок в триадах.
Связи в сети практически всегда являются ориентированными, поскольку отношения, представленные взвешенными связями, не должны быть симметричными.
Обыкновенные графы используются для представления взаимоотношений между объектами в пространстве или во времени. Можно использовать их и для представления более абстрактных причинно-следственных связей, как, например, связей между различными видами патологий в медицине (рис. 6.2). Доступ к такой информации связан в той или иной мере с использованием специальных средств прослеживания путей на графе, для которых разработаны самые различные алгоритмы (см., например, работу [Pearl, 1984]).
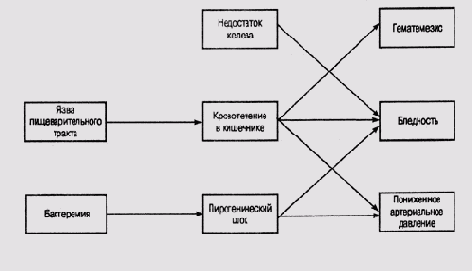
Рис. 6.2. Участок сети причинно-следственных связей ([Pople, 1982P
Для представления иерархических классификаций и сетей применяются деревья. Например, на рис. 6.3 показано дерево классификации болезней по расположению пораженного органа. Корневой узел дерева представляет множество всех болезней, а его наследники — группы болезней, соответствующие основному пораженному органу. Каждый из этих узлов будет иметь своих наследников, представляющих более узкие группы болезней, и т.д. Терминальные узлы дерева будут представлять конкретные заболевания.
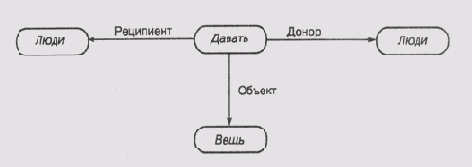
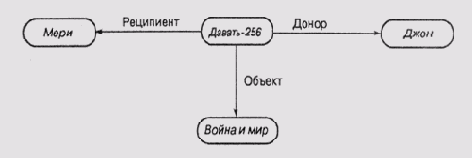
Семантические сети вначале использовались для представления смысла выражений естественного языка человека, откуда и появилось название этого класса сетей. Теперь же они используются в качестве структуры, пригодной для представления информации общего вида, — узлы представляют некоторые концепты (понятия), а связи — отношения между концептами. На рис. 6.4 представлены два фрагмента семантической сети. Первый фрагмент представляет глагол давать и показывает, что этот глагол может иметь три вида взаимодействия с остальными членами предложения: с донором, реципиентом и с объектом, который должен быть передан. Надписи в узлах, к которым подходят связи, соответствуют классу сущностей, которые могут выступать в качестве субъектов связи. Так, донор и реципиент, как правило, —люди, а то, что нужно передать, — вещь.
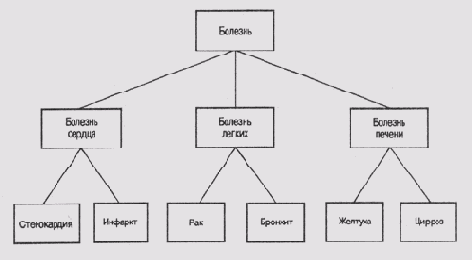
Рис. 6.3. Обыкновенное дерево классификации болезней
a
б
Рис. 6.4. Фрагменты семантической сети: а) представление глагола "давать "; б) представление конкретного действия
Второй фрагмент соответствует конкретной фразе или конкретной реализации действия, означенного этим глаголом. Эту реализацию мы назвали давать-265. Смысл фразы состоит в том, что Джон передает Мери книгу "Война и мир". Фразу можно считать допустимой, поскольку все ее члены удовлетворяют ограничениям, специфицированным соответствующими узлами сети. Джон и Мери принадлежат к классу люди, а "Война и мир" — к классу книга, который, в свою очередь, является одним из видов класса вещи.
Обычно узел давать-265 связывается с узлом давать связью, которая указывает, что давать-265 — это одна из конкретных реализаций концепта (в данном случае действия) давать. Такого рода специальные связи часто называют ISA-связями (связями типа "это есть...").
Термин ассоциативные сети лучше отражает характер использования такого рода формальных структур для тех задач, которые мы рассматриваем. Поскольку аппарат ассоциативных сетей все шире используется для моделирования объектов и их взаимосвязей в конкретных предметных областях, что необходимо для построения экспертных систем, ниже мы рассмотрим их более детально.
Множественное наследование
В то определение понятия наследования, которое было дано в работах Квиллиана, концепция фреймов внесла определенные коррективы. В настоящее время является общепризнанным, что некоторый фрейм может наследовать информацию от множества предшественников в системе фреймов. В результате граф, представляющий связи между фреймами, стал больше походить на решетку, чем на дерево, поскольку каждый узел не обязательно имеет единственного предшественника. Очень часто система строится таким образом, что некоторые фреймы имеют несколько предшественников, хотя в подавляющем большинстве структур сохраняется единственность корня. Пример такой структуры представлен на рис. 6.7.
Новый узел Правильный многоугольник "не вписывается" в прежнюю классификацию, в которой за основу бралось количество сторон. Этот фрейм вводит в систему новый атрибут— "правильность" контура фигуры. Таким образом, появляется возможность передать таким фреймам, как Квадрат и Равносторонний треугольник, некоторые свойства, характерные именно для равносторонних фигур, использовав для этого механизм множественного наследования. Например, все равносторонние многоугольники имеют равные значения внутренних углов, и лучше всего хранить информацию об этом свойстве именно во фрейме Правильный многоугольник, как это следует из принципа когнитивной экономии.
Такая организация связей между фреймами не влечет за собой никаких проблем только до тех пор, пока информация, поступающая от различных источников наследования, не становится противоречивой. Но рассмотрим пример, представленный на рис. 6.8. (Он часто используется в специальной литературе и даже получил имя собственное — "Алмаз Никсона", по причинам, которые станут ясны далее.)
Положим, мы договорились считать по умолчанию, что квакеры — это пацифисты, т.е. в слоте пацифизм фрейма квакер "прописано" значение истина, и что республиканцы пацифистами не являются, т.е. в слоте пацифизм фрейма республиканец "прописано" значение ложь.
Все это означает, что при отсутствии более полной информации о каком-либо конкретном республиканце или квакере предполагается, что он именно так относится к идеям пацифизма.
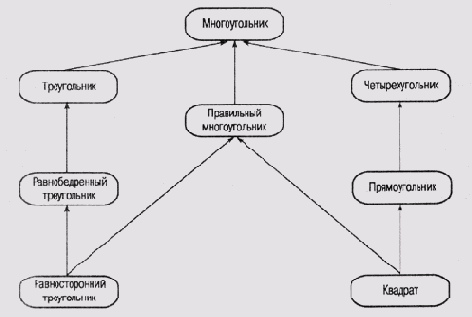
Рис. 6.7. Гетерархическое представление множества геометрических фигур

Рис. 6.8. Конфликт при множественном наследовании свойств
Но что в таком случае можно сказать о квакере, который является сторонником Республиканской партии? А ведь именно в такой роли выступал бывший Президент США Ричард Никсон. Является ли он пацифистом или нет? Иными словами, откуда должен унаследовать квакер-республиканец значение слота пацифизм, если считать, что мы не располагаем никакой дополнительной уточняющей информацией?
Поскольку значения, предлагаемые по умолчанию, конфликтуют друг с другом, мы, используя только ранее введенную информацию, не можем ничего сказать о пацифизме Ричарда Никсона. В такой ситуации некоторые системы, использующие механизм наследования, отказываются давать однозначное заключение. Системы с таким поведением получили наименование скептических (см., например, [Horty et al, 1987]). Другие, обнаружив подобный конфликт, выносят заключение наудачу. За ними закрепилось определение доверчивые (см., например, [Touretzky, 1986]).
Трудно отдать предпочтение какой-либо из этих стратегий. Но в любом случае лучше заранее подумать о том, как избежать подобных конфликтов при внедрении систем фреймов. Например, можно оспорить мнение, что миролюбивый республиканец — явление более редкое, чем квакер, поддерживающий акции с применением силы, и либо установить определенный порядок анализа наследования от различных предшественников, либо не использовать в данном случае механизм наследственности и принудительно установить значение истина для слота пацифизм во фрейме квакер-республиканец. Есть и альтернативный вариант— подключить к слоту пацифизм во фрейме квакер-республиканец специальный демон по требованию, использующий "для устранения неоднозначности какие-либо "посторонние" знания, которыми мы не располагаем на стадии конструирования системы фреймов.
Так, квакер- республиканец может не следовать идеям пацифизма в год выборов в соответствии с общей политикой своей партии, но в обычное время будет рассматриваться как пацифист, полагая, что квакерское воспитание пересиливает партийную дисциплину.
Следует отметить, что анализ сетей с наследованием оказывается проще, чем анализ систем фреймов, поскольку узлы в сети не нуждаются в слотах или подключенных процедурах. Неоднозначность в сети устанавливается путем анализа ее топологии. Для того чтобы в сети потенциально могла появиться неоднозначность, о которой идет речь, необходимо, чтобы набор узлов {А, В, С, ...} образовал ациклический граф со связями двух типов: положительные связи, которые означают, что А является элементом В, и отрицательные связи, которые означают, что А не является элементом В. Тогда мы сможем представить проблему выяснения глубины пацифистских взглядов Р. Никсона в виде сети рис. 6.9. Здесь пацифист — это узел со своими собственными правами, и отрицательный характер связи между ним и узлом республиканец показан засечкой на линии связи.
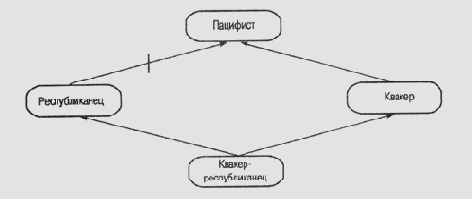
Рис. 6.9. Представление "проблемы Никсона" в виде сети с наследованием
Из изложенного ясно, что в гетерархической системе потенциальные возможности для образования самых разнообразных взаимосвязей гораздо шире, чем в системе с жесткой иерархической структурой. Узлы более высоких уровней могут иметь общих наследников на более низких уровнях, что является признаком существования непрямых отношений между такими узлами. Например, имеются определенные отношения между узлами, представляющими равносторонний треугольник и квадрат в рассмотренном выше примере. В системе фреймов значение некоторого слота также может быть указателем на определенный фрейм (или фреймы), что порождает еще одно измерение в структуре системы (см. об этом в описании системы CENTAUR в главе 13).
Основные понятия концепции фреймов
6.3.1. Основные понятия концепции фреймов
Становление теории систем фреймов во многом обязано ряду интуитивных предположений, касающихся механизмов психологической деятельности человека. В частности, предполагается, что представление понятий в мозге не требует строгого формулирования набора свойств, которыми должна обладать та или иная сущность, чтобы можно было рассматривать ее в качестве представителя определенной категории сущностей. Многие из тех категорий, которыми мы пользуемся, не имеют четкого определения, а базируются на довольно расплывчатых понятиях. Создается впечатление, что человек более всего обращает внимание на те бросающиеся в глаза свойства, которые ассоциируются с объектами, наиболее ярко представляющими свой класс.
Такие объекты были названы "прототипическими объектами", или прототипами. В частности, "прототипическая" птица, например воробей, может летать, а потому у нас есть основание полагать, что это — свойство всех птиц, хотя и существуют редкие виды птиц, которые этим свойством не обладают, например пингвины. Именно в этом смысле воробей является лучшим экземпляром категории "птицы", чем пингвин, поскольку он представляет более типические свойства объектов своего класса. Несмотря на существование видов птиц, являющихся исключением в своем классе, мы можем сформулировать обобщенное свойство объектов этого класса следующим образом: "птицы летают".
Теперь обратимся к объектам другого рода— математическим, например многоугольникам. По отношению к этой категории объектов у нас также имеется интуитивное представление о типичности. Например, рассматривая четырехугольники, представленные на рис. 6.5, вряд ли кто будет оспаривать утверждение, что "типичность" объектов увеличивается по мере перехода от фигур, расположенных слева, к фигурам, расположенным справа. Четырехугольник, не обладающий выпуклостью, кажется нам менее типическим, чем выпуклый, а прямоугольник кажется более типическим, чем выпуклый четырехугольник с различными внутренними углами, возможно потому, что площадь фигуры коррелируется в нашем сознании с длиной периметра, а эта связь лучше проявляется при равных значениях внутренних углов.
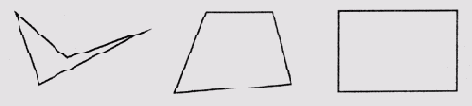
Рис. 6.5. Изменение "типичности" прямоугольников разного вида
В системе фреймов предпринимается попытка судить о классе объектов, используя представление знаний о прототипах, которые хорошо представляют большинство разновидностей объектов данного класса, но должны быть каким-то образом скорректированы, для того чтобы представить всю сложность, присущую реальному миру. Так, если мне ничего не известно о площади более или менее прямоугольного участка земли, но известны длины сторон, то я могу оценить площадь, полагая, что внутренние углы контура этого участка почти равны. В худшем случае, если мои предположения о равенстве углов окажутся уж слишком далеки от действительности, то оценка площади будет завышенной, но такая ситуация типична для подавляющего большинства эвристических механизмов.
При решении практических проблем мы встречаемся с изобилием исключений из правил, а границы между разными классами оказываются очень размытыми. Системы фреймов оказываются полезными по той причине, что они дают нам в руки средства структурирования эвристических знаний, связанных с приложением правил и классификацией объектов. При использовании фреймов эвристические знания не "размазываются" по программному коду приложения, но и не собираются воедино в виде метазнаний, а распределяются между теми видами объектов, к которым они приложимы, и существуют на уровне управления в иерархии представления таких объектов.
Представление типовых объектов и ситуаций
В этом разделе мы рассмотрим более простой механизм представления знаний, названный системой фреймов. Этот механизм появился в результате стремления объединить декларативные знания об объектах, о событиях и их свойствах и процедурные знания о методах извлечения информации и достижения целей. Предполагалось, что механизм фреймов поможет избежать ряда проблем, связанных с представлением на основе семантических сетей.
Разделение видов узлов и когнитивная экономия
6.2.1. Разделение видов узлов и когнитивная экономия
Два аспекта модели памяти, предложенной Квиллианом, оказали особенно существенное влияние на последующее развитие исследований в области применения систем семантических сетей.
Во-первых, он ввел разделение между видами узлов, представляющих концепты. Один вид узлов он назвал узлами-типами. Такой узел представляет концепт, связанный с конфигурацией других узлов, узлов-лексем. Конфигурация узлов-лексем образует определение концепта узла-типа. Это в определенной степени напоминает толковый словарь, в котором каждое понятие (элемент словаря) определяется другими понятиями, также присутствующими в этом словаре, причем их смысл толкуется с помощью еще каких-либо понятий в этом словаре. Таким образом, смысл узла-лексемы определяется ссылкой на соответствующие узлы-типы.
Например, можно определить смысл слова "машина" как конструкцию из связанных компонентов, которые передают усилие для выполнения некоторой работы. Это потребует присоединения узла-типа для слова "машина" к узлам-лексемам, представляющим слова "конструкция", "компонент" и т.д. Однако в дополнение к связям, сформированным для определения смысла, могут существовать и связи к другим узлам-лексемам, например "телетайп" или "офис". Эти связи представляют знание о том, что телетайпы являются одним из видов машин, которые используется в офисе.
Другое интересное свойство модели памяти получило наименование когнитивной экономии. Суть его поясним на примере. Если известно, что машина — это конструкция, состоящая из взаимодействующих деталей, а телетайп — это тоже машина, то можно сделать вывод, что телетайп — это тоже конструкция. Таким образом, нет смысла в явном виде хранить эту информацию, присоединяя ее к узлу "телетайп". Указывая, что этот узел сохраняет определенные свойства, заданные связями узла "машина", мы можем сэкономить память и сохранить при этом возможность извлечь всю необходимую информацию, если только будем способны построить правильную схему влияния одних узлов на другие.
Эта схема, которую в настоящее время принято называть схемой наследования свойств, получила широкое распространение в представлении знаний. Наследование свойств является типичным примером сохранения объема памяти за счет снижения производительности, которое должен учитывать разработчик схемы представления знаний. Мы увидим в дальнейшем, что такой подход влечет за собой появление множества нетривиальных проблем, в частности, если допустить возможность исключений в наследовании, т.е. существование таких узлов-лексем, которые не наследуют все свойства своего узла-типа. Кроме того, хотя смысл понятий полностью определен в пределах сети, но для каждого отдельного понятия он "размазывается", т.е. отдельные части определения связываются с разными узлами. В нашем примере определение понятия "телетайп" только частично хранится в соответствующем узле, а остальная часть определения находится в узле "машина".
Таким образом, помимо антагонизма "объем памяти/производительность", появляется еще и антагонизм между модульностью определения и разумностью этого определения с точки зрения пользователя. Тем не менее, если эта идея будет корректно реализована, программа всегда будет знать, как отыскать отдельные части определения некоторой сущности и собрать их воедино. Главное же преимущество состоит в том, что в узле можно хранить произвольное количество семантической информации, например данные о диапазонах значений свойств, которыми могут обладать узлы-лексемы определенного типа. В чистом виде такая организация памяти не практикуется при использовании формализмов вроде продукционных систем, поскольку придется выполнять трудоемкий анализ целостности информации в рабочей памяти либо с привлечением специальных правил, описывающих такую целостность, либо с помощью самих правил поиска решений. В любом случае это потребует значительных вычислительных ресурсов.
В двух сборниках [Bobrow and Collins, 1975] и [Findler, 1979] содержится подборка статей, которые дают достаточно полное представление об исследованиях, выполненных в то время, когда проблематика ассоциативных сетей вызывала наибольший интерес. Начинать изучение концепции фреймов следует с пионерской статьи Минского, опубликованной в сборнике [Winston, 1975], в которой даны исходные формулировки базовых понятий, таких как "типичность" и "значения по умолчанию". Другие понятия, связанные с этой концепцией, рассматриваются в работе Шенка и Абельсона [Schank and Abelson, 1977].
Турецкий рассмотрел некоторые теоретические вопросы построения сетей с наследованием и предложил весьма интересную процедуру формирования суждений при наличии исключений [Touretzky, 1986]. Среди более поздних работ, посвященных этим проблемам, следует отметить [Touretzky et al, 1987], [Horty et al., 1987] и [Selman and Levesque, 1989]. В последней статье показано, что предложенная Турецким процедура относится к классу NP-hard, т.е. для обширных сетей с большим количеством связей становится "вычислительно необозримой".
Позднее Томасон опубликовал обзор современных работ по сетям с наследованием [Thomason, 1992], а в двух работах Йена описана методика интеграции концепции сетей с наследованием в экспертные системы, основанные на порождающих правилах [Yen et al., 1991,a], [Yen et al, 1991, b].
Сравнение сетей и фреймов
Подводя итог всему сказанному выше об ассоциативных сетях и фреймах, отметим, что в большинстве предлагаемых структур сетей не удалось дать четкий ответ на два важных вопроса.
Что же действительно стоит за узлами и связями в сети?
Как можно эффективно обрабатывать информацию, хранящуюся в такой структуре?
В большинстве последних исследований, касающихся представления знаний, предпочтение отдается фреймам. Такой подход дает вполне удовлетворительные ответы на сформулированные выше вопросы. Семантика узлов и связей четко прослеживается благодаря разделению узлов на узлы-типа и узлы-лексемы и ограничению количества связей. Эффективность обработки обеспечивается подключением к узлам специфических процедур, на которые возлагается вычисление значений переменных в ответ на запросы или при обновлении значений других свойств узла.
Использование фреймов в качестве основной структуры данных, хранящей информацию о типичных объектах и событиях, в настоящее время широко распространено в практике создания приложений искусственного интеллекта (см. об этом в главах 13 и 16). Большинство программных инструментальных средств, предназначенных для построения экспертных систем, обеспечивает тем или иным способом организацию базы знаний на основе фреймов (см. об этом подробнее в главах 17 и 18). Во многих случаях желательно оценить, какими возможностями обладает механизм представления гипотез с помощью фреймов в части использования таких данных, как совокупность симптомов или результатов наблюдений за поведением объектов. Сопоставление этих данных с информацией, хранящейся в слотах фреймов, предоставляет свидетельство в пользу гипотез, представленных фреймом, а также позволяет формулировать определенные предположения относительно других данных, например предположить существование дополнительных симптомов, присутствие или отсутствие которых сможет подтвердить (или опровергнуть) анализируемую гипотезу (см. об этом подробнее в главе 13).
Естественно, для того чтобы реализовать систему фреймов в виде, пригодном для работы с конечным пользователем, требуется разработать программную оболочку и средства пользовательского интерфейса. Хотя к слотам отдельных фреймов и могут быть подключены специальные процедуры, эти локальные модули не способны взять на себя все заботы об организации вычислительного процесса в системе. Необходимо иметь в той или иной форме специальный интерпретатор, который будет формировать и обрабатывать запросы и принимать решение, при каких условиях можно считать достигнутой цель, сформулированную в запросе. Поэтому чаще всего фреймы используются в сочетании с другими средствами представления знаний, в частности в сочетании с порождающими правилами. В следующей главе мы рассмотрим стиль программирования, который в определенной степени избавляет структурированные объекты от необходимости пользоваться внешними средствами контроля, поскольку позволяет объектам пересылать сообщения друг другу и инициировать таким образом более сложные вычисления.
Как вы думаете, можно ли
1. Прочитайте статью Хейеса в сборнике [Brachman and Levesque, 1985]. Как вы думаете, можно ли считать фреймы не более чем средством реализации подмножества логики предикатов, или они позволяют смоделировать экстралогические свойства, присущие человеку, формулирующему суждения?
2. Неоднозначность, которую мы обнаружили в "проблеме Никсона", можно распространить каскадно и получить еще более замысловатые примеры. Один из них взят из работы [Touretzky et al., 1987] (рис. 6.10). Познакомьтесь с этой работой, а затем ответьте на следующие вопросы.
I) К какому заключению придет доверчивый резонер, рассуждая об отношении квакера-ре спубликанца к армии?
II) К какому заключению придет резонер-скептик?
3. Примеры сетей с наследованием, представленные на рис. 6.11 и 6.12, также взяты из работы [Touretzky et a/., 1987]. На этих рисунках представлены две топологически
идентичные сети, которые отличаются только маркировкой узлов. На рис. 6.11 показано, что королевские слоны являются исключениями, поскольку не имеют серой окраски, а на рис. 6.12 показано, что капелланы являются исключениями, поскольку это мужчины, не склонные к употреблению пива.
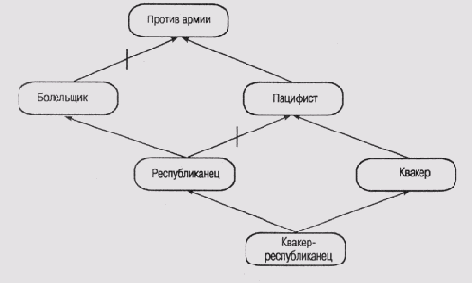
Рис. 6.10. Сеть с наследованием, в которой имеется каскад неоднозачностей
I) Резонер Турецкого должен был бы заключить, что в обоих случаях возможно несколько интерпретаций. Согласны ли вы с таким заключением или нет и по какой причине?
II) Сандуол полагает, что корректная интерпретация сети на рис. 6.11 состоит в том, что прямой путь от узла королевский слон к узлу серые животные должен иметь более высокий приоритет, чем непрямой путь через узел слон [Sandewall, 1986]. А что вам подсказывает ваша интуиция?
III) Днализируя сеть, представленную на рис. 6.12, Турецкий пришел к заключению, что изменение маркировки узлов сети с одной и той же топологией меняет и наше интуитивное предположение о распространении наследуемых свойств. Заключение о том, что корабельный капеллан не является любителем пива (как на том настаивает Сандуол), является менее обоснованным, чем в случае со слонами.
В пользу такого заключения Турецкий приводит следующие аргументы.
Ни капелланы, ни моряки не могут рассматриваться как типичные мужчины, причем обе категории очень сильно отличаются друг от друга. Поэтому сделать какое-либо заключение о свойствах корабельного капеллана очень сложно.
Хотя нам и известно, что капелланы — трезвенники, мы ничего не знаем о том, насколько распространено употребление пива среди моряков на кораблях. Вполне возможно, что оно стало популярным и среди корабельных капелланов.
С какой из участвующих в споре сторон согласны вы? Или, возможно, у вас есть аргументы в пользу обеих точек зрения?
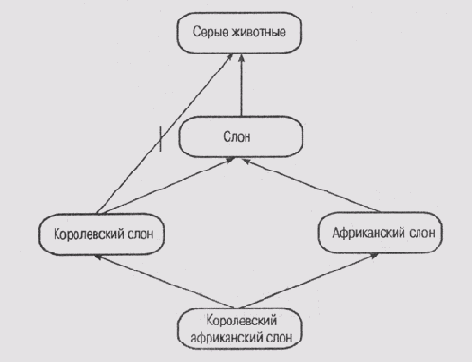
Рис. 6.11. Проблема "королевского слона"
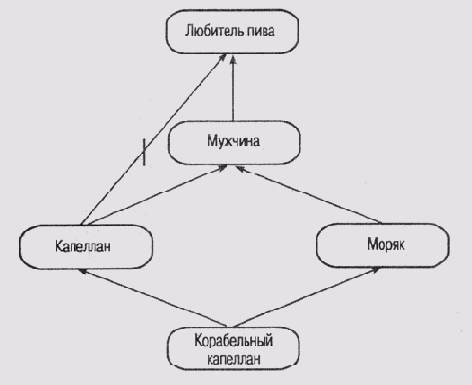
Рис. 6.12. Проблема "корабельного капеллана "
4. Просмотрите пример из врезки 6.1. Придумайте обработчик сообщения для класса square, который будет вычислять площадь объекта этого класса, например объекта square-one, а затем присваивать вычисленное значение слоту этого объекта.
Для этого вам понадобится сначала внести изменения в определение класса square.
(defclass square (is-a rectangle)
(slot length-of-sides (create-accessor write))
(slot area (create-accessor write)))
Согласно этому определению, класс square имеет два слота: length-of-sides — для хранения длин сторон объекта, area — для хранения его площади. Фацет create-accessor в определении слота говорит о том, что функции доступа к слоту должны автоматически формироваться средствами языка CLIPS. Последние самостоятельно сформируют объявления функций put-length-of-sides и put-area. Эти наименования функций можно затем использовать в обработчиках сообщений.
Второй шаг — модифицировать спецификацию объекта, в которую следует включить задание длин сторон:
(definstances geometry (square-one of square
(length-of-sides 10)))
Теперь остается только разработать обработчик события, который будет использовать функцию для установки нужного значения в слот area объекта square-one.
5. Метод, который был реализован в предыдущем упражнении, хорош для работы с квадратами, но с его помощью нельзя решить аналогичную проблему при работе с другими четырехугольниками, представленными в нашей иерархии,— прямоугольниками, параллелограммами и трапециями.Теперь, когда вы знаете, как сформировать слоты и обработчики событий, пользуясь средствами языка CLIPS, попытайтесь решить и эту проблему. Для этого вам потребуется передавать объекту любого класса, расположенного в иерархии ниже узла четырехугольник, сообщение, в ответ на которое соответствующий обработчик должен извлечь данные из слотов, представляющих отдельные исходные параметры формы фигуры (длины сторон, высота и т.д.), и обрабатывать их по формуле, специфичной для фигур каждого вида. Постарайтесь найти такое решение, которое позволяло "бы обрабатывать различные фигуры по возможности единообразно. Учтите, что подклассы могут наследовать и слоты, и обработчики сообщений от своих суперклассов (предшественников).
Значения по умолчанию и демоны
Представьте себя на некоторое время в роли агента по оценке недвижимости. Вы должны оценить примерную стоимость на рынке земельных участков, полной информацией о которых не располагаете. Большинство участков имеет, как правило, форму выпуклых прямоугольников, поэтому можно оценить стоимость участков, предполагая, что те, о которых идет речь, также имеют подобную форму, если только у вас нет конкретной информации об обратном.
Предположим, что граф на рис. 6.6 представляет знания о плоских геометрических фигурах, которые можно использовать для логических рассуждений о форме участков. Каждый узел на этом графе имеет связанную с ним структуру записей (фрейм), формат которой приведен ниже.
NAME (ИМЯ):
Number of sides (Количество сторон):
Length of sides (Длины сторон):
Size of Angles (Углы):
Area (Площадь):
Price (Цена):
Практически все слоты фрейма Многоугольник придется оставить незаполненными, поскольку ничего нельзя сказать о сторонах и углах типичного многоугольника. Однако для слота Количество сторон в качестве значения по умолчанию можно установить 4, поскольку подавляющее большинство земельных участков имеет форму четырехугольника. Таким образом, все земельные участки, информация о форме контура которых отсутствует, будут полагаться четырехугольными. Слот Площадь также нельзя заполнить, но известно, как вычислить площадь многоугольника, располагая другой информацией о нем. Любой n-сторонний многоугольник можно разбить на п-2 треугольника, вычислить их площади и затем просуммировать результаты. Программу, реализующую эту процедуру, можно подключить к слоту Площадь. Процедуры, подключенные к структуре данных и запускаемые на выполнение при появлении запроса или обновлении информации в структуре, иногда называют демонами. Те демоны, которые по запросу вычисляют некоторые значения, называются демонами по требованию (IF-NEEDED).
Полезно также иметь демон, который при заполнении слота Площадь сразу вычислял бы цену участка. Эта процедура относится к другому типу демонов — демонам добавления (IP-ADDED) — и подключается также к слоту Площадь.
Теперь при обновлении или установке значения слота Площадь автоматически будет вычислена цена участка, а результат будет помещен в слот Цена.
Перейдем к следующему уровню в иерархии фреймов. Для фрейма Четырехугольник совершенно очевидно нужно установить значение 4 в слот Количество сторон. Это значение будет наследоваться фреймами на каждом из последующих уровней иерархии. Вычислять площадь и цену всех фигур, представленных фреймами последующих уровней, можно тем же способом, что и для многоугольника. Поэтому описанные выше демоны также могут быть унаследованы всеми последующими фреймами.
Но для четырехугольника можно примерно оценить площадь, даже не располагая информацией о значениях внутренних углов контура, а зная только длины сторон. Вполне приемлемые результаты можно получить с помощью следующего эвристического способа: среднюю длину стороны для одной пары противолежащих сторон умножить на среднюю длину стороны для другой пары. Этот метод даст существенную ошибку только для четырехугольников, не являющихся выпуклыми, а такое встречается очень редко.
Эта эвристика может быть реализована в виде демона по требованию, подсоединенного к слоту Площадь фрейма Четырехугольник. Такой демон должен выполнять следующее:
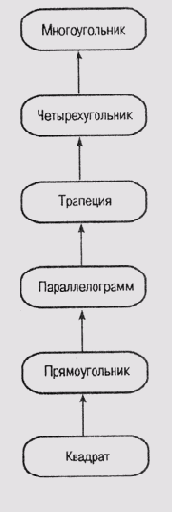
Рис. 6.6. Иерархия плоских геометрических фигур
если имеется информация о величинах углов четырехугольника и длинах сторон, то вызывать демон фрейма Многоугольник и выполнять точное вычисление площади;
если имеется только информация о длинах сторон четырехугольника, то выполнять вычисление по приближенному эвристическому методу;
если отсутствует любая информация о параметрах четырехугольника, не выполнять никаких вычислений.
Фреймы, представляющие все последующие разновидности четырехугольников, наследуют значение из слота Количество сторон фрейма Четырехугольник. Но в каждом из этих фреймов можно реализовать свою процедуру вычисления площади, лучше учитывающую особенности именно данного вида фигур. Например, площадь трапеции можно вычислить как произведение высоты на среднюю длину оснований, а фреймы прямоугольника и квадрата могут унаследовать эту процедуру у параллелограмма, площадь которого равна произведению основания на высоту.
Этот простой пример демонстрирует, как, используя значения по умолчанию и демоны, можно заполнить слоты иерархической системы фреймов, причем этот механизм оказывается более удобным, чем тот, который используется в структурах записей языка PASCAL. Данные, процедуры и определения оформляются в виде единого пакета и образуют отдельный модуль для каждого фрейма, причем разные модули могут совместно использовать данные и процедуры, пользуясь механизмом наследования.
6.1. Реализация фреймов и наследования в языке CLIPS
Хотя язык CLIPS и не поддерживает в явном виде формализм семантических сетей и фреймов, их можно неявно определить, используя имеющуюся в CLIPS конструкцию def class. Мы более подробно поговорим об этой конструкции в следующей главе, поскольку ее основное назначение — реализация объектно-ориентированного подхода. Для представления иерархии геометрических объектов, показанной на рис. 6.6, нам понадобятся следующие определения:
(defclass polygon (is-a USER))
(defclass quadrilateral (is-a polygon))
(defclass trapezium (is-a quadrilateral))
(defclass parallelogram (is-a trapezium))
(defclass rectangle (is-a parallelogram))
(defclass square (is-a rectangle))
Обратите внимание на то, что класс polygon (многоугольник) объявлен как подкласс класса USER, который является базовым для всех классов, объявленных пользователем. Отношение is-a (является), которое фигурирует во всех языках представления фреймов, обычно обладает свойством транзитивности: квадрат является прямоугольником, но квадрат также является и трапецией и т.д. Это отношение является антисимметричным, т.е. если квадрат является прямоугольником, то прямоугольник в общем случае не является квадратом.
Для того чтобы представить на языке CLIPS тот факт, что большинство многоугольников предположительно должно иметь четыре стороны, потребуются кое-какие дополнительные языковые конструкции. Нужно будет несколько изменить определение классов polygon и quadrilateral:
(defclass polygon (is-a USER)
(role abstract)
(slot no-of-sides (default 4)))
(defclass quadrilateral (is-a polygon)
(role concrete))
Теперь polygon объявлен как абстрактный класс, т.е. класс, не способный самостоятельно порождать определенные объекты. Его подкласс quadrilateral и все последующие подклассы класса quadrilateral являются конкретными классами, т.е. эти классы могут порождать конкретные экземпляры (объекты классов). При определении класса polygon его слоту no-of-sides (количество сторон) назначено по умолчанию значение 4. Это отражает наше интуитивное предположение, что большинство многоугольников будет четырехугольниками. В терминологии систем фреймов такое значение по умолчанию называется фацетом слота no-of-sides.
После этого можно приступить к описанию демонов. Для этого нужно воспользоваться конструкцией defmessage-handler, которая имеется в CLIPS. (Подробно конструкция defmessage-handler также будет описана в следующей главе.)
(defmessage-handler polygon sides () ?self:no-of-sides)
Демон sides связан с классом polygon и попросту получает доступ к слоту no-of-sides того объекта, который его вызвал. Предположим, например, что определен конкретный участок, имеющий форму квадрата, причем ему присвоено наименование square-one.
(definstances geometry (square-one of square))
Система инициализируется командой (reset). Теперь можно активизировать демон, послав ему сообщение
(send [square-one] sides)
В ответ интерпретатор CLIPS выведет результат
Обратите внимание на то, что выражение ?self :no-of-sides вычисляется в контексте объекта square-one, которому было направлено сообщение и который в ответ на него активизировал демона. В этом выражении ?self является переменной и определяет объект, к слоту которого производится обращение, а двоеточие — это инфиксный оператор доступа к конкретному слоту.
Язык KRL
В языке KRL впервые была сделана попытка собрать воедино результаты выполненных ранее исследований о структурировании элементов знаний и реализовать их в виде единой системы [Bobrow and Winograd, 1977]. Создание системы преследовало не только теоретические цели, но и имело достаточно четкую практическую направленность. В качестве "строительных блоков" системы использованы так называемые "концептуальные объекты", которые были сходны с фреймами, предложенными Минским, в том, что представляют прототипы и связанные с ними свойства. Основную идею авторы так изложили в опубликованной в 1977 году статье:
"...анализ последствий объектно-центрической факторизации знаний в противовес более общей факторизации, предполагающей структурирование знаний в виде набора фактов, каждый из которых ссылается на один или несколько объектов".
Такая ориентация повлекла за собой создание декларативного языка, основанного на описаниях, в которых концептуальные объекты рассматриваются не изолированно, а в совокупности с другими объектами-прототипами. Фундаментальное предположение состояло в том, что то, какие свойства некоторого объекта знаний оказываются существенными, представляющими интерес и т.д., зависит от точки зрения на объект и цели решаемой задачи. Например, если вам нужно сыграть музыкальную пьесу на пианино, то вас интересуют такие свойства этого объекта, как качество звучания, настройки и т.п. А вот грузчику более интересны такие свойства этого музыкального инструмента, как вес и габариты.
В этом свете описание новой сущности можно рассматривать как процесс сравнения ее с ранее описанными: нужно указать, на какие из известных объектов похож новый и чем именно, а в чем от них отличается. Так, мини-фургон очень похож на легковой автомобиль, но отличается от последнего отсутствием сидений для пассажиров и окон в задней части. Другими словами, полный набор понятий можно определить в терминах друг друга, а не в терминах более компактного множества примитивных идей.
Сложность с использованием примитивов в представлении семантики состоит в том, что вряд ли когда-нибудь удастся прийти к единому мнению о том, что же представляют собой такие примитивные понятия и как их следует комбинировать при формировании более сложной идеи (с некоторыми соображениями на сей счет читатель может ознакомиться в работах [Schank, 1975] и [Schank andAbelson, 1977]).
В основе процедурных свойств языка KRL также лежат наиболее распространенные программные методы, предполагающие подключение процедур общего вида к классам объектов данных. Бобров и Виноград объединили этот вид подключения процедур со структурой фрейма и позволили подклассам наследовать как процедуры, так и данные своего суперкласса.
Разработчики языка предположили, что наследование процедур позволит программировать в терминах родовых операций, детали реализации которых конкретизируются по-разному для объектов разных классов. Так же, как абстрактные типы данных позволяют программисту забыть о деталях хранения конкретных данных в машине, так и родовые операции позволяют на определенной стадии не принимать во внимание детали реализации однотипных операций в каждом конкретном случае. Пример поможет вам четче представить смысл этой идеи.
Предположим, вас назначили Верховным главнокомандующим при проведении военной операции, в которой принимают участие различные рода войск. Отданные в ваше распоряжение танки, корабли и самолеты ждут приказа атаковать. Получив такой приказ, каждый из родов войск будет действовать по-своему: самолеты начнут бомбить, корабли — выпускать ракеты и т.д. Но поведение каждого из родов войск — это частная реализация общей концепции наступательных военных действий. Как главнокомандующего, вас мало интересуют детали выполнения приказа: на какие рычаги нажимать, какие переключатели включать, — все это должно быть определено на более низких уровнях.
Возвращаясь вновь к KRL, отметим, что идея, которая стоит за объектно-центрической организацией процедур, состоит в том, чтобы попытаться программно воспроизвести тот естественный стиль выработки суждений, который реализуется в мозге человека.
В частности, предполагается, что управление логическим выводом реализуется на локальном уровне, в отличие от глобальных задач, ассоциирующихся, например, с автоматическим доказательством теорем. Другими словами, зная, как реализовать родовые операции, классы объектов будут обладать знаниями и о том, когда активизировать те многочисленные процедуры, к которым они имеют доступ.
Мы не затрагивали многих других аспектов языка KRL, например средств управления процессом или составления расписаний работ. Читателям, интересующимся этим языком, рекомендуем познакомиться с критическим анализом этого языка, который выполнили Ленерт и Уилкс [Lehnert and Wilks, 1979], и ответом разработчиков на эти критические замечания [Bobrow and Winograd, 1979]. Нельзя не отметить, что язык KRL явился тем локомотивом, который существенно подтолкнул исследования в области теории представления знаний и, в частности, способствовал появлению практических систем, о которых речь пойдет в следующем разделе.
7.1. Процедуры и объекты
На рис. 7,1 мы попытались схематически представить, в чем основная разница между процедурно- и объектно-ориентированным подходами в программировании.
Серые! эллипсы на схеме в левой части рисунка представляют процедуры, некоторые из которых напрямую обращаются к данным, хранящимся в файле или в базе данных. Зачерненный эллипс представляет процедуру самого верхнего уровня (в языке С — это процедура main). Эта функция вызывает другие функции, которые в конце концов вызывают функции самого нижнего уровня, выполняющие операции ввода/вывода.
На правой схеме объекты объединяют данные и процедуры работы с ними. Объекты организованы в виде одной или нескольких иерархических структур — деревьев или решеток. Утолщенный прямоугольник на схеме представляет базовый абстрактный класс. Экземпляры этих объектов взаимодействуют друг с другом, обмениваясь сообщениями, и таким образом образуются связи, ортогональные иерархии наследования.
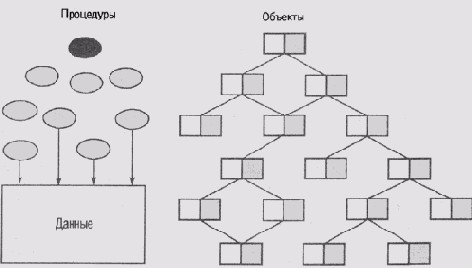
Рис. 7.1. Процедурно- и объектно-ориентированные парадигмы программирования.Незаполненные фигуры представляют данные, а фигуры с заливкой—процедуры
Языки CLIPS и CLOS
Появление языка Common LISP было связано с попыткой стандартизировать многочисленные диалекты LISP и создать устраивающую большинство пользователей версию этого языка. Развитие объектно-ориентированного подхода в программировании привело к разработке объектно-ориентированной версии LISP — Common LISP Object System (CLOS), о которой и пойдет речь в этом разделе. Разработчики CLOS включили в свою систему поддержку всех новшеств, ранее хорошо себя зарекомендовавших в языках FLAVORS и LOOPS, таких как множественное наследование, объединение методов и структура метаклассов.
Объектно-ориентированная версия CLIPS, язык COOL, очень близок к CLOS, что мы и продемонстрируем на примерах в этом разделе.
Языки LOOPS и FLAVORS
Объектно-ориентированный стиль программирования идеально подходит для решения проблем, требующих детального представления объектов реального мира и динамических отношений между ними. Классическим примером применения данного подхода являются задачи моделирования. В таких программах компоненты сложной системы представляются структурами, инкапсулирующими и данные, и функции, моделирующие поведение соответствующих компонентов. Первым языком, в котором была реализована такая идея, стал SmallTalk [Goldberg andRobson, 1983].
Для задач искусственного интеллекта были разработаны языки LOOPS и FLAVORS, причем оба представляли собой объектно-ориентированные расширения языка LISP. Хотя в настоящее время эти языки практически не используются, реализованные в них базовые идеи унаследованы множеством языков представления знаний, появившихся позже. В частности, это можно сказать о языках CLOS (Common LISP Object System) и CLIPS. Ниже мы кратко опишем основные функциональные возможности языков LOOPS и FLAVORS и обратим ваше внимание на некоторые сложности, связанные с реализацией объектно-ориентированного стиля программирования.
Метаклассы
Отличительной чертой языка LOOPS является поддержка концепции метаклассов, т.е. классов, членами которых являются другие классы. Впервые метаклассы появились в языке SmallTalk. В первой системе реализации этого языка имелся единственный метакласс Class, членами которого были все прочие классы в системе, в том числе и Class. В более поздних реализациях SmallTalk метакласс формировался автоматически всякий раз, когда создавался новый класс, и этот класс становился экземпляром класса Metaclass. Метаклассы в SmallTalk-80 сами по себе не являлись экземплярами метаклассов, а принадлежали единственному метаклассу Metaclass. Во избежание путаницы мы в дальнейшем будем называть "классами объектов" те классы, которые не являются метаклассами.
Смысл существования метаклассов — поддержка создания и инициализации экземпляров классов. Обычно сообщение посылается экземпляру класса, а не самому классу. Экземпляр класса наследует поведение от своего класса объектов. Но иногда желательно передать сообщение именно классу, например сообщение "сформировать экземпляр с такими-то свойствами". Классы наследуют поведение от своих метаклассов и таким образом вся система обладает приятным с точки зрения пользователя единообразием. (Обычно сообщения метаклассам не посылаются, но если такое произойдет, то они будут наследовать поведение от класса Metaclass, к которому они все принадлежат, включая и сам Metaclass.)
В языке LOOPS метакласс не создается для каждого класса. Этот язык имеет более простую структуру классов, представленную схематически на рис. 7.4. Узлы в форме эллипсов представляют классы объектов и метаклассы, а узлы в форме прямоугольников представляют экземпляры классов объектов. Тонкие стрелки означают отношения вида "А является подклассом В", а толстые — отношения вида "А является экземпляром В".
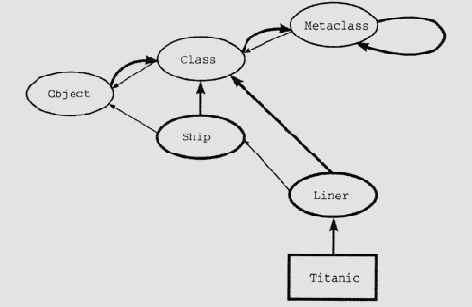
Рис. 7.4. Структура классов в языке LOOPS
LOOPS поддерживает три стандартных метакласса: Object, Class и Metaclass. Тонкие стрелки на рис. 7.4 означают, что Object является суперклассом класса Class, a Class является суперклассом класса Metaclass.
Кроме того, Object является членом Class, Class — членом Metaclass, a Metaclass — членом самого себя. Таким образом, оказывается, что Object является корнем иерархии классов (не имеет суперкласса), а Metaclass является корнем иерархии экземпляров (не имеет ни одного класса, кроме самого себя).
Узлы, вычерченные утолщенными линиями — ship (корабль) и liner (лайнер), — типичные классы, определенные пользователем. Обратите внимание на то, что все классы такого рода являются членами класса Class, от которого они наследуют свое поведение. Таким образом, для того чтобы сформировать экземпляр Titanic, нужно переслать сообщение new классу liner, который наследует метод new от класса Class. Поведение экземпляра Titanic, естественно, будет унаследовано от его класса— в данном случае liner.
Использование метаклассов позволяет запрограммировать поведение по умолчанию и определенные виды структур в объектно-ориентированной системе на самом высоком уровне. Экземпляры классов объектов, таких как liner, обычно формируются стандартным способом, но если для одного или семейства классов желательно использовать какой-то более специфический вариант, нужно включить между liner и Class определенный пользователем метакласс (например, metaliner), в котором и "прописать" желаемые модификации (рис. 7.5). Таким образом, структура классов в языке LOOPS позволяет в одной системе объединить мощность и гибкость представления объектов реального мира.
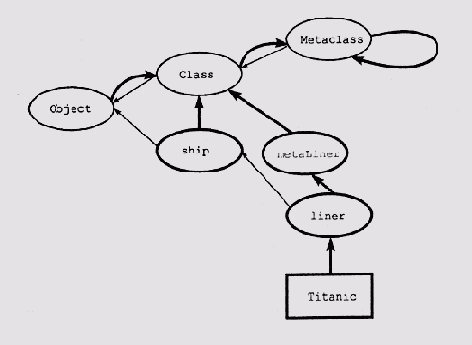
Рис. 7.5. Вставка метакласса, определенного пользователем
Метаклассы в CLOS и CLIPS
В языке CLOS классы и метаклассы интегрированы в среду LISP. Фактически каждый объект LISP является экземпляром класса. Например, существует класс массивов array, соответствующий типу данных array в Common LISP.
В CLOS поддерживаются три базовых метакласса.
standard-class. Это метакласс по умолчанию для любого класса объектов, определенных пользователем с помощью функции defclass. Ниже приведено определение обычного класса father (отец), который имеет суперклассы man (мужчина) и parent (родитель), слоты для хранения имени (name) и рода занятий (occupation) экземпляров класса, а также краткого описания (documentation).
(defclass father (man parent) (:name)
(:occupation) (:documentation "Класс родителя мужского пола"))
Большинство классов, определенных пользователем, имеет именно этот метакласс.
build-in-class. Это метакласс тех классов объектов, которые реализованы необычным способом. Например, некоторые из таких классов могут соответствовать типам данных Common LISP. Большинство системных классов имеет именно этот метакласс.
structure-class. Это метакласс тех классов объектов, которые определены с помощью функции defstruct, а не defclass. Функция defstruct используется в Common LISP для формирования фреймов, состоящих из слотов и наполнителей, но не поддерживающих множественное наследование.
Хотя функциональные возможности базовых метаклассов вполне приемлемы для большинства приложений, программист может воспользоваться и опциями формирования специализированного standard-class, который будет обладать каким-нибудь экзотическим поведением. В частности, можно использовать meta-object protocols (протоколы мета-объектов) и переопределить родовой алгоритм диспетчирования. В результате у разработчика появляется возможность создать собственный механизм наследования, более приемлемый для конкретного приложения, чем стандартный. Нужно отметить, что подобного рода возможности отсутствуют в языках, подобных C++, правда, как показал опыт, большинство пользователей обращаются к ним очень редко.
Язык COOL, включенный в состав CLIPS, имеет 17 системных классов, причем некоторые из них выполняют функции метаклассов. Верхние уровни структуры классов схематически представлены на рис. 7.7.
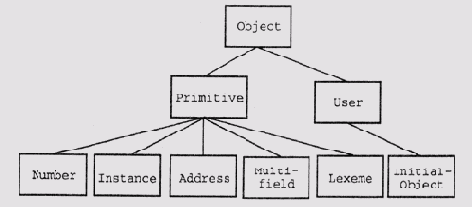
Рис. 7.7. Верхние уровни иерархической системы классов языка COOL
Все классы, определенные пользователем, являются производными от USER, который отчасти выполняет функции метакласса. В нем реализованы практически все базовые обработчики сообщений инициализации и удаления объектов. Однако USER все-таки не является метаклассом, поскольку классы, определенные пользователем, — это производные от USER, а не его экземпляры. Initial-Object является экземпляром по умолчанию, который создается при выполнении функции def instaces. Класс Primitive и его подклассы реализуют основные структуры данных — числа, символы строки, адреса и многокомпонентные объекты. Все классы, представленные на рис. 7.7, кроме Initial-Object, являются абстрактными и служат только для определения родовых операций и структур данных.
Множественное наследование в C++
Так же, как язык CLOS представляет собой объектно-ориентированное расширение языка LISP, так и язык C++ создан на основе широко известного языка С и сохранил все его возможности, добавив к ним средства объектно-ориентированного программирования. Если отвлечься от того факта, что CLOS и C++ основаны на разных языках-прототипах, то основное отличие между ними заключается в реализации механизма наследования, в частности множественного наследования. В языке C++ множественное наследование трактуется совсем не так, как мы это делали в предшествующих разделах настоящей главы, а потому этот вопрос заслуживает подробного обсуждения.
В языке C++ родовые операции реализуются в виде виртуальных функций. Виртуальная функция, объявленная в классе X, это функция, которая может быть перегружена (переопределена) в классе, производном от X. При объявлении в классе X виртуальная функция вообще может не иметь тела, т.е. программного кода реализации. В таком случае функция называется чисто виртуальной, а класс, имеющий одну или более чисто виртуальных функций, является абстрактным базовым классом, экземпляры которого создать невозможно. В любом случае ключевое слово virtual говорит компилятору, что программный код функции будет уточнен в производных классах.
Те методы, которые вызываются на выполнение, являются невиртуальными членами-функциями, т.е. функциями, имеющими определенный программный код, который не перегружается в производных классах. В этом смысле C++ существенно отличается от языка CLOS, в котором практически все функции суперкласса в большей или меньшей степени модифицируются механизмом наложения методов. Поэтому в C++ существует множество синтаксических тонкостей, в которых не нуждается CLOS. Например, во всех классах иерархии виртуальная функция должна иметь квалификатор virtual до тех пор, пока в некотором производном классе не будет представлена ее конкретная реализация.
В чисто иерархической структуре классов, когда каждый производный класс имеет единственного "родителя", передача методов по наследству выполняется совершенно очевидным способом.
Единственная тонкость в реализации этого механизма в C++ состоит в использовании квалификаторов наследования public и private. Если не вдаваться в подробности, то наследование вида public представляет собой отношение "is а" (является), которое мы использовали при обсуждении фреймов. Наследование вида private ближе к отношению "реализовано в терминах", которое позволяет скрыть определенные детали реализации интерфейсов объектов. Такое полезное разделение "выпало" в языке CLOS, в котором каждое отношение "класс-подкласс" несет семантический смысл.
Но если обратиться к множественному наследованию, то механизмы его реализации в C++ и CLOS существенно отличаются. Поскольку в языке C++ не существует такого понятия, как порядок предшествования классов, то даже такой простой случай, как в рассмотренном выше примере "Алмаз Никсона", приводит к неоднозначности. Будем считать, что отношения между классами Person, Quaker, Republican и Republican_Quaker, как и прежде, имеют вид, представленный на рис. 7.8.
Объявление классов Person, Quaker, Republican и Republican Quaker на языке C++ показано в листинге 7.2 (программный код объявления включен в файл nixon.h).
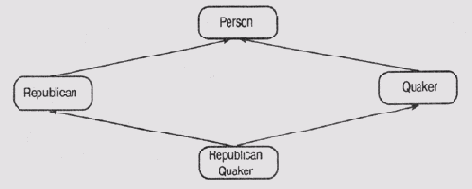
Рис. 7.8. Отношения между классами в примере "Алмаз Никсона"
Листинг 7.2. Файл nixon.h. Объявление классов, версия 1
// Объявление классов для задачи "Алмаз Никсона" finclude <iostream.h>
class Person
{ public:
Personf) {};
virtual "Person() {};
virtual void speak() = 0; };
class Republican : public Person
{ public:
Republican)) {};
virtual ~Republican)) {};
virtual void speak() { cout « "War";} };
class Quaker : public Person
{ public:
Quakerf) {};
virtual ~Quaker)) {};
virtual void speak)) { cout « "Peace";} };
class Republican_Quaker : public Republican,
public Quaker
{ public:
Republican_Quaker() {};
virtual ~Republican_Quaker() {};
};
Создадим экземпляр richard класса Republican_Quaker.
#include "nixon.h" void main))
Republican_Quaker richard; richard.speak));
При обработке этого программного кода компилятор C++ обнаружит, что вызов richard.speak)) содержит неоднозначную ссылку. Оно и понятно, поскольку нельзя однозначно заключить, скажет ли Ричард "War" (война) или "Peace" (мир).
Если мы решим, что метод speak)) класса Republican_Quaker должен "брать пример" с класса Quaker, то проблему можно решить, определив этот метод одним из двух способов:
void S::speak(){ cout << "Peace"; }
или
void S::speak)({Quaker::speak)); }
Первый вариант просто перегружает оба наследованных определения метода, а второй в явном виде вызывает один из них, а именно тот вариант, который реализован в классе Quaker.
Однако совершенно незначительное на первый взгляд изменение в файле определения классов может разительно изменить поведение объекта. Предположим, решено удалить объявления методов speak)) из всех классов, кроме Person, как это показано в листинге 7.3.
Листинг 7.3. Файл nixon.h. Объявление классов, версия 2
class Person
public:
Person)) {};
virtual "Person)) {};
virtual void speak)){ cout « "Beer";}
};
class Republican : public Person
public:
Republican)) {}; virtual ~Republican)) {};
class Quaker : public Person
public:
Quaker)) {};
virtual ~Quaker)) {};
class Republican Quaker : public Republican, public Quaker
{
public:
Republican_Quaker( ) {} ;
virtual ~Republican_Quaker( ) {};
}
При обработке такого файла определения компилятор опять выдаст сообщение о неоднозначности ссылки на метод speak ( ). Это произойдет по той причине, что компилятор сформирует две копии объявления класса Person — по одной для каждого пути наследования, а это приведет к конфликту имен. Чтобы устранить эту неоднозначность, нужно объявить Person как виртуальный базовый класс и для Republican, и для Quaker. Тогда оба производных класса будут ссылаться на единственный объект суперкласса (листинг 7.4).
Листинг 7.4. Файл nixon.h. Объявление классов, версия 3
class Person
{ public:
Per son () {};
virtual "Person)) {};
virtual void speak(){ cout << "Beer";} И
class Republican : virtual public Person
{ public:
Republican)) {};
virtual ~Republican)) {};
};
class Quaker : virtual public Person
{
public:
Quaker)) {};
virtual ~Quaker)) .{};
}
class Republican_Quaker : public Republican, public Quaker
{
public:
Republican_Quaker { ) { } ;
virtual "Republican_Quaker( ) {};
}
Объявление Person в качестве виртуального базового класса для Republican и Quaker имеет и еще одно преимущество. Предположим, что нам нужно сделать так, чтобы класс Republican_Quaker отдавал предпочтение стилю поведения квакеров, а все другие были индифферентны к вопросам войны и мира и следовали линии поведения, определенной классом Person. Тогда, поскольку Person является виртуальным базовым классом, можно заставить доминировать Quaker::speak)) над Person::speak)) для класса Republican_Quaker (листинг 7.5).
Листинг 7.5. Файл nixon.h. Объявление классов, версия 4
class Person
public:
Person)) {};
virtual ~Person)) {};
virtual void speak)){ cout « "Beer";}
class Republican : virtual public Person
public:
Republican)) {}; virtual ~Republican)) {};
class Quaker : virtual public Person
public:
Quaker)) {};
virtual ~Quaker() {};
virtual void speak)) { cout « "Peace";}
class Republican_Quaker : public Republican, public Quaker
public:
Republican_Quaker() {};
virtual "Republican_Quaker() {};
}
При создании языка C++ преследовалась цель не усложнять механизм множественного наследования по сравнению с единственным и разрешать все неоднозначности на стадии компиляции [Stromtrup, 1977]. В этом существенное различие между C++ и SmallTalk. В последнем такого рода конфликты разрешаются на стадии выполнения программы. Это также отличается и от метода, основанного на списке предшествования классов, который используется в CLOS.
Кроме того, в языке CLOS конфликта имен, подобного тому, который мы наблюдали с классом Person, быть просто не может, поскольку все базовые классы с одинаковыми именами считаются идентичными.
Таким образом, за высокую эффективность языка C++ приходится платить, тщательно продумывая передачу свойств и поведения от классов родителей к производным классам с учетом всех нюансов функционирования механизма наследственности в C++.
В этом отношении C++ напоминает свой прототип — язык С, который требует гораздо более близкого знакомства с работой компьютера, чем язык LISP, поскольку позволяет напрямую обращаться к памяти компьютера, манипулировать адресами, формировать собственный механизм выделения памяти и т.д. Какую стратегию предпочесть — зависит от индивидуальных предпочтений разработчика, но если главным требованием к продукту является высокая производительность, то чем большими возможностями управления ресурсами обладает разработчик, тем лучше, тем более эффективную программу можно создать.
Суммируя все сказанное о языке C++, отметим, что он вполне может послужить базовым программным инструментом для создания экспертных систем. Если потребуется интерпретатор порождающих правил, то можно либо разработать его самостоятельно (хотя это и далеко не тривиальная задача), либо воспользоваться одним из имеющихся на рынке, которые допускают внедрение в среду C++. Если вам удастся избежать описанных выше сложностей в реализации множественного наследования, вы сможете в полной мере воспользоваться многочисленными преимуществами этого языка — проверкой статических типов, разделением между закрытым и общедоступным наследованием, множеством средств защиты данных от случайных изменений.
Множественное наследование в CLOS и CLIPS
Механизм множественного наследования в языках CLOS и CLIPS работает практически так же, как и в языке LOOPS. Порядок, в котором базовые классы перечислены в определении подкласса, задает и порядок приоритетов наследования данных и процедур. Кроме того, существует правило, в соответствии с которым определение процедуры или свойства, сделанное в классе, всегда имеет приоритет перед унаследованными от суперклассов. Эти соглашения позволяют разрешить проблему неоднозначности при множественном наследовании путем формирования списка предшествования классов.
Рассмотрим фрагмент программы на языке CLIPS, представленный в листинге 7.1. Этот фрагмент описывает "Алмаз Никсона", о котором шла речь в главе 6. Класс person определен как объявленный пользователем, классы quaker и republican — производные от person, a republican-quaker — производный как от quaker, так и от republican. Класс USER является системным абстрактным классом, т.е. может быть использован только для создания подклассов. Если планируется создавать экземпляры любого класса, производного от USER, то этот класс нужно объявлять с квалификатором concrete, как это и сделано при объявлении класса republican-quaker.
Листинг 7.1. Объявление классов на языке CLIPS
(defclass person (is-a USER)
(defclass quaker (is-a person)
(defclass republican (is-a person)
(defclass republican-quaker
(is-a republican quaker) (role concrete)
Список предшествования классов для класса republican-quaker будет иметь вид (republican-quaker republican,quaker person).
Список формируется в результате прослеживания графа связей системы классов, который неявно представлен слотами is-a в определениях классов.
Роль списка предшествования классов становится ясной при разработке обработчика событий для производного класса. Определим поведение классов quaker и republican как "голубей" и "ястребов" соответственно:
(defmessage-handler quaker speak () (printout t crlf "Peace")
)
(defmessage-handler republican speak ()
(printout t crlf "War") )
Сформируем экземпляр класса republican-quaker:
(definstances people
(richard of republican-quaker))
Теперь загрузим все это в исполняющую систему CLIPS и введем запрос к экземпляру Richard:
(send [richard] speak)
В ответ интерпретатор выведет "War" (война). Оказывается, что "ястребиный" характер республиканцев возобладал у экземпляра richard, поскольку в списке предшествования классов republican стоит раньше, чем quaker. Изменим порядок перечисления этих классов в определении republican-quaker:
(defclass republican-quaker
(is-a quaker republican)
(role concrete) )
Теперь в характере экземпляра Richard миролюбие квакеров будет доминировать. Ничего не изменится в поведении экземпляра и в том случае, если добавить обработчик сообщения в класс person:
(defmessage-handler person speak ()
(printout t crlf "Beer") )
Эта реализация метода speak перекрывается другими, поскольку класс находится в списке предшествования на последнем месте.
Слоты данных в языке COOL также поддерживают фацеты, т.е. свойства, ответственные за доступ к слотам в процессе работы программы. Например, существует фацет visibility (видимость), который определяет, какие другие классы могут обратиться к слоту. Значение private означает, что только обработчик сообщения данного класса может получить доступ к данным, а значение public позволяет это сделать также обработчикам сообщений производных классов и суперклассов.
Другие фацеты позволяют реализовать следующие возможности:
автоматическое определение функций доступа и присвоения значений слотам;
хранение данных, к которым возможен доступ со стороны всех экземпляров класса, аналогично статическим членам классов в языке C++.
Наложение методов в CLOS и CLIPS
В языках FLAVORS и LOOPS реализованы разные механизмы комбинирования поведения, унаследованного от разных "родителей". В языке FLAVORS используется описанный выше механизм вставок, а в языке LOOPS производится дополнительное обращение к альтернативному коду.
В языке CLOS поддерживаются оба варианта. Обычно существует главный метод, который берет на себя основную часть работы по выполнению родовой операции (примером является метод refresh, о котором шла речь при обсуждении набора классов окон). Как и в языке FLAVORS, before-методы (предварительные методы) используются для подготовки данных для тех вычислений, которые должны быть выполнены primary-методом (основным методом), а after-методы (заключительные-методы) используются для выполнения заключительных операций.
Кроме того, в CLOS имеется возможность использовать так называемые around-методы (методы оболочки), которые образуют своего рода оболочку вокруг ядра (последовательности "before-метод— primary-метод— after-метод"). Такая методика предназначена для ситуаций, в которых ядро не позволяет достичь требуемого результата. Например, желательно, чтобы before-метод установил локальные переменные, которые должны быть использованы primary-методом, или когда нужно заключить primary-метод в какую-либо управляющую структуру. В ядре before- и after-методы используются только для того, чтобы сформировать побочные эффекты; возвращается же значение, сформированное primary-методом, причем это значение не ограничивается никакими внешними управляющими структурами.
Наиболее специфический around-метод связывается с сообщением, которое передается перед тем, как будут вызваны подходящие before-, primary- или after-методы. Обращение к ядру производится в процессе выполнения системной функции call-next-method, которая размещается в теле around-метода.
Стандартная методика наложения методов суммирована в схеме, представленной на рис. 7.6.
В CLOS предлагается множество дополнительных типов наложения методов.
Более того, пользователь может самостоятельно создавать и собственные типы. Например, тип or-combination передает вызывающему объекту значение первого компонента, вернувшего значение, отличное от NIL. При создании собственных функций наложения пользователь может использовать операторы разных видов: логические, арифметические или манипулирования списками.
Следует отметить, что стандартная схема наложения методов удовлетворяет потребности программирования практически на 90%.
Методы в CLOS являются эффективными родовыми функциями, возможность применения которых зависит от специальных параметров, представляющих класс первого аргумента сообщения. Методы вызываются точно так же, как и функции LISP (т.е. не используются никакие функции отсылки, как это делается в LOOPS). Получатель сообщения представляется первым аргументом, а остальные'аргументы — обычные параметры функции.
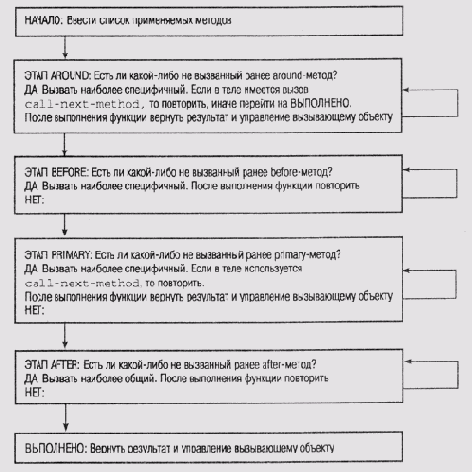
Рис. 7.6. Стандартная схема наложения методов в языках CLOS и CLIPS ([Keene,1989])
Кроме того, в CLOS существуют и так называемые мультиметоды, которые позволяют настраивать поведение в зависимости от классов нескольких аргументов, а не одного. Например, люди, принадлежащие к разным культурам, не только отдают в своем рационе приоритет разным продуктам, но и готовят их по-разному. Так, японцы, в отличие от американцев, отдают предпочтение рыбе, но, кроме того, они часто едят рыбу сырой. Таким образом, метод prepare-meal (приготовить пищу) должен быть чувствителен как к национальности получателя сообщения, так и к виду предлагаемого блюда. Метод имеет два аргумента
(prepare-meal X Y)
и его реализация зависит как от класса аргумента X (повара), так и от класса аргумента У (блюда). Аналогичные возможности в CLIPS обеспечиваются посредством родовых функций (подробнее об этом — в главе 17).
7.3. Как сделать людей вежливыми
Положим, что используются те же обработчики сообщений для классов guaker и republican, что и в предыдущем примере. Можно, определив специальный заключительный метод для класса person, придать формируемым ответам вежливый вид.Этот метод будет выполняться после того, как будет выполнен основной метод, выбранный для ответа на сообщение speak:
(defmessage-handler guaker speak ()
(printout t crlf "Peace")
)
(defmessage-handler republican speak ()
(printout t crlf "War")
)
(defmessage-handler person speak after()
(printout t ", please" t crlf)
)
Теперь в ответ на запрос (send frichard] speak) последует ответ "War, please" Обработчики сообщений базовых классов имеют статус primary по умолчанию, а потому можно и не указывать это явно в объявлении обработчика, как это сделано, например, ниже:
(defmessage-handler republican speak primary () (printout t crlf "War")
Объектно-ориентированное программирование
7.1. Язык KRL
7.2. Языки LOOPS и FLAVORS
7.3. Языки CLIPS и CLOS
7.4. Множественное наследование в C++
7.5. Объектно-ориентированный анализ и конструирование экспертных систем
Рекомендуемая литература
Упражнения
За последние 20 лет было разработано довольно много языков для представления знаний, причем большинство из них можно отнести к классу объектно-ориентированных. Как и в случае с использованием концепции фреймов, основная идея состоит в том, чтобы заключить данные и связанные с ними процедуры в некие структуры, объединенные механизмом наследования. Отличие от формализмов, описанных в предыдущей главе, состоит в том, что процедуры могут наследоваться (и комбинироваться) точно так же, как и данные, а объекты могут взаимодействовать друг с другом напрямую или посредством специальных протоколов обмена сообщениями.
Сначала читатель вкратце познакомится с одним из предшественников современных программных средств — системой KRL (сокращение от Knowledge Representation Language — язык представления знаний). Потом будет показано, как в процессе эволюции в последующих разработках были преодолены некоторые сложности, присущие этому стилю программирования. Читатель познакомится с системами FLAVORS, LOOPS и более современной системой CLOS (Common LISP Object System — объектная система на базе обычного LISP). В конце главы описывается, как объектно-ориентированный подход реализован в языке CLIPS, и рассмотрены достоинства и недостатки использования для представления знаний объектно-ориентированных языков общего назначения, таких как C++.
В данной главе мы вновь затронем некоторые вопросы, рассмотренные в предыдущих главах, в частности вопрос о наследовании, но уделим ему гораздо больше внимания. Независимо от того, какой конкретный язык будет обсуждаться в том или ином разделе, во всех представленных примерах используется либо язык COOL (CLIPS Object Oriented language — объектно-ориентированная версия языка CLIPS), либо C++. Разделы, в которых детально изложены технические подробности функционирования конкретных программных средств (они помечены крестиком), можно при желании опустить. Большинство примеров приведено во врезках. При первом чтении их также можно бегло просмотреть или опустить, что не помешает разобраться в основных темах главы.
Объектно-ориентированный анализ и конструирование экспертных систем
Философия и технология объектно-ориентированного программирования могут весьма пригодиться проектировщику экспертных систем.
Философия представления знаний о реальном мире в терминах взаимодействия объектов и субъектов предоставляет достаточно удобную среду для решения большого класса проблем, предполагающих значительный объем моделирования (задачи планирования и составления расписаний).
Методика представления абстрактных данных и процедур позволяет программистам, занятым задачами искусственного интеллекта, на ранних этапах разработки сосредоточиться на выборе подходящих видов объектов и их поведении, не вдаваясь в подробности реализации функций и структур данных.
Существует довольно много литературы по объектно-ориентированному программированию, которая поможет конструктору экспертных систем.
Но существуют и определенные сложности внедрения объектно-ориентированного подхода в область задач искусственного интеллекта.
Объекты в основном являются средствами реализации вычислений.
Идея наследования поведения вленет за собой появление множества проблем при ее реализации, как мы видели это на примере с классами окон. Некоторые из появившихся в последнее время объектно-ориентированных схем допускают наследование только интерфейсов.
Определенные сложности возникают с реализацией наследования при использовании новых технологий многокомпонентных объектов, таких как СОМ (см. [Chappell, 1996]).
В идеальном случае желательно так организовать разработку системы, особенно экспертной, чтобы добавление новых возможностей сводилось к включению в систему новых модулей программного кода. Приведенные в этой главе примеры показывают, что это вряд ли возможно даже при использовании объектно-ориентированной среды. Добавление новых модулей знаний всегда связано с побочными эффектами, которые вовлекают в свою орбиту правила разрешения конфликтов и неопределенностей. В дальнейшем мы покажем, что эта проблема характерна и для технологии логического программирования (об этом речь пойдет в главе 8).
Таким образом, совершенно очевидно, что реализация идей объектно-ориентированного программирования не позволяет решить все проблемы и разработчику экспертной системы будет еще над чем поломать голову. Но объектно-центрическая парадигма упрощает принятие определенных видов решений в процессе проектирования системы и облегчает реализацию уже принятых.
Передачсообщений
Идея объектно-ориентированного программирования состоит в том, что программа строится вокруг множества объектов, каждый из которых обладает собственным набором функций (операций). Вместо того чтобы представлять объект пассивным набором данных, объектно-ориентированная система позволяет объекту играть более активную роль, в частности взаимодействовать с другими объектами, обмениваясь с ними сообщениями. В результате основной упор переносится с разработки общей управляющей структуры программы, которая ответственна за порядок обращения к функциям, на конструирование самих объектов, выяснение их ролей и создание протоколов взаимодействия объектов. Эти протоколы, по существу, определяют интерфейс между объектами. Если один объект должен взаимодействовать с другим, он должен вызывать функции в строгом соответствии с этим интерфейсом.
Объекты располагают собственными данными, которые играют ту же роль, что и слоты фреймов, собственным механизмом обновления этих данных и использования хранящейся в них информации. Помимо функций интерфейса, объекты располагают собственными, "приватными" функциями, которые, как правило, представляют собой реализацию определенной родовой операции применительно к данному объекту. Помимо данных, передаваемых в качестве аргументов родовой операции, такие функции используют и локальные данные объекта — аналоги слотов фрейма.
Предположим, мы определили объект, представляющий класс ship (корабль), и наделили его свойствами x-velocity (скорость по х) и y-velocity (скорость по у). Теперь можно создать экземпляр класса ship, назвать его Titanic и одновременно присвоить свойствам x-velocity и y-velocity нового экземпляра исходные значения. Практически нет никаких отличий между этой процедурой и процедурой создания нового экземпляра фрейма, рассмотренной в предыдущей главе.
Предположим теперь, что нам понадобилось определить процедуру speed, которая будет вычислять скорость судна на основании значений свойств x-velocity и у-velocity (скорость вычисляется как корень квадратный из суммы квадратов компонентов).
Такая процедура будет принадлежать абстрактному типу данных, представляющему любые суда (в терминологии языка SmallTalk speed — это метод класса ships, а в терминологии C++ — функция-член класса ships.)
Идея состоит в том, чтобы закодировать в объекте (классе) не только декларативные знания о судах, но и процедурные, т.е. методы использования декларативных знаний. Для того чтобы активизировать процедуру вычисления скорости определенного судна, в частности "Титаника", нужно передать объекту Titanic сообщение, которое побудит его обратиться к ассоциированной процедуре в контексте данных о компонентах скорости именно этого объекта. Titanic — это экземпляр класса ships, от которого он унаследовал процедуру speed. Все это представляется довольно очевидным, но описанный механизм срабатывает только в случае, если соблюдаются следующие соглашения.
Во-первых, программа, разработанная в расчете на этот механизм, должна "учредить" и следовать в дальнейшем определенному протоколу или "контракту", определяющему способ взаимодействия между объектами. Другими словами, интерфейс обмена сообщениями между объектами должен быть досконально продуман, а правила этого интерфейса жестко соблюдаться. Лучше всего продемонстрировать эту мысль на примере.
Для того чтобы определить компоненту X текущего положения "Титаника", программа должна послать запрос объекту Titanic, который имел бы следующий смысл: "передай текущее значение координаты X". Как в объекте формируется это значение или как оно хранится — дело только самого объекта и никого более не касается. Ни объекты других классов, ни какие-либо другие компоненты программы этого не знают. Более того, внутренний механизм доступа к этой информации должен быть скрыт, чтобы никто не мог добраться к ней, минуя сам объект. Это соглашение принято называть инкапсуляцией.
Во-вторых, совершенно очевидна избыточность определения своего метода вычисления скорости для каждого класса объектов, которые обладают возможностью перемещаться в двумерной системе координат.
Метод, который мы только что определили для класса судов, с таким же успехом может быть использован и для других движущихся объектов, поскольку вычисление скорости представляет собой родовую операцию. Поэтому имеет смысл связать этот метод с каким-нибудь суперклассом транспортных средств, производными от которого будут классы судов, автомобилей, троллейбусов и т.п. Все эти подклассы унаследуют родовую операцию у своего базового класса.
Такое наследование — это уже нечто большее, чем когнитивная экономия или наследование свойств. Выполнение родовых операций встраивается в механизм обмена сообщениями. Отсылка сообщения— это отнюдь не вызов определенной процедуры, поскольку вызывающий объект не знает, каким именно методом отреагирует на это сообщение объект-получатель, от кого он унаследует этот метод, и будет ли вообще задействован механизм наследования в данном конкретном случае. Вызывающему объекту известны лишь наименование операции и ее внешние по отношению к преемнику аргументы. Все остальное — заботы объекта-реципиента сообщения.
7.2. Формирование объекта класса на языке CLIPS
Ниже показано, как на языке CLIPS определяется класс ship и формируется экземпляр этого класса titanic. Сначала определим класс ship, в котором имеются два слота: x-velocity и y-velocity:
(defclass ship
(is-a INITIAL_OBJECT)
(slot x-velocity (create-accessor read-write))
(slot y-velocity (create-accessor read-write)) )
Теперь сформируем экземпляр этого класса,, которому будет дано наименование "Titanic". Проще всего это сделать с помощью функции definstaces, которая в качестве аргументов принимает список параметров формируемых экземпляров. Определенные таким способом экземпляры класса будут инициализироваться при каждом перезапуске интерпретатора CLIPS.
(definstances ships (titanic of ship
(x-velocity 12) (y-velocity (10)
Завершается определение созданием обработчика событий для класса ship. Все экземпляры класса будут использовать этот обработчик для вычисления собственной скорости.Обратите внимание на то, что член в этом определении ссылается на значение слота того экземпляра класса, скорость которого требуется вычислить.
(defmessage-handler ship speed () (sqrt
( +
{ ?self:x-velocity ?self:x-velocity)
( ?self:y-velocity ?self:y-velocity)))
)
Если файл со всеми представленными выше выражениями загрузить в среду CLIPS, а затем ввести с клавиатуры (send [titanic] speed), то в ответ интерпретатор CLIPS выведет скорость объекта titanic.
Проблемналожения методов
Та простая картина, которая вырисовывается из представленного выше механизма прямого наследования, несколько усложняется, если мы попытаемся заменить прямое наследование множественным. В главе 6 уже отмечалось, что это может привести к неоднозначности в наследовании свойств. Но в контексте объектно-ориентированного подхода при множественном наследовании появляется и неоднозначность поведения.
С этой проблемой впервые столкнулись при разработке объектно-ориентированного языка FLAVORS, который поддерживает множественное наследование и наложение методов [Cannon, 1982]. Язык FLAVORS позволяет объектам иметь несколько родителей и таким образом наследовать процедуры и данные из нескольких источников. Для FLAVORS характерна не иерархия объектов, а гетерархия. Если графически изобразить отношения между разными объектами в FLAVORS, то схема будет больше походить на решетку, чем на дерево. Каков во всем этом смысл? Рассмотрим следующий пример, взятый из статьи Кэннона.
Отображение окон на дисплее рабочей станции реализуется, как правило, с использованием объектно-ориентированного стиля программирования. Будем считать, что окна на экране дисплея представлены в виде LISP-объектов, в каждом из которых записаны свойства окна (размеры и положение на поле экрана) и процедуры работы с окном (открытие, закрытие, перерисовка и т.п.). Существует несколько разновидностей окон и соответственно объектов окон — с рамкой, без рамки, со строкой заголовка, без заголовка и т.д.
Класс окно с рамкой .является подклассом (или производным классом) класса окно. Точно так же подклассом класса окно является и класс окно с заголовком. В иерархической системе классы окно с рамкой и окно с заголовком представляют собой отдельные узлы одного и того же уровня иерархии. Они наследуют определенные методы, например refresh (освежить), от базового класса окно, но имеют и собственные методы выполнения таких операций, как перерисовка рамки или строки заголовка.
А теперь предположим, что нам потребовался еще один вид окна — окно с рамкой и строкой заголовка.
Окно такого типа должно быть представлено новым классом окно с рамкой и заголовком. В иерархической системе новый класс будет наследником класса окно и независимым "близким родственником" уже существующих классов окно с рамкой и окно с заголовком на том же уровне иерархии (рис. 7.2). Но даже интуитивно чувствуется, что такая организация избыточна. Ведь фактически мы стремимся "смешать" два набора уже существующих качеств и получить в результате новый комбинированный набор. Кажется, что целесообразнее сделать новый класс "дитятей" двух родителей, — классов окно с рамкой и окно с заголовком (рис. 7.3).
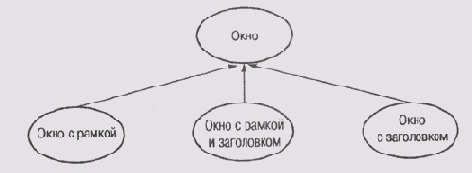
Рис. 7.2. Иерархическая система классов окон
Но здесь возникают вопросы: а как новый класс будет наследовать процедуры, определенные в двух базовых классах? Устроит ли нас "смешанное" поведение нового класса? Эту проблему можно разложить на две составляющие:
найти подходящие методы в базовых классах;
скомбинировать их таким образом, чтобы получить желаемый эффект.
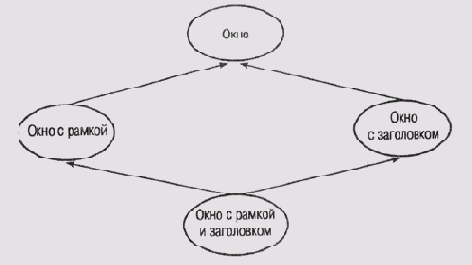
Рис. 7.3. Гетерархическая система классов окон
Для решения этой задачи очень подходит механизм включения в основной метод вставок, которые должны выполняться до или после него. В приведенном выше примере с объектами окон можно скомпоновать метод отрисовки окна с рамкой и строкой заголовка таким образом, чтобы новый класс использовал унаследованный от класса окно метод refresh и, кроме того, специализированные методы, унаследованные от каждого из ближайших родителей и выполняемые после основного refresh. При этом должен четко соблюдаться порядок выполнения унаследованных операций и вставок, поскольку его изменение может привести к нежелательному эффекту. В нашем примере после выполнения метода "прародителя" окно нужно выполнить сначала вставку, унаследованную от класса окно с рамкой, а потом вставку, унаследованную от класса окно с заголовком. В противном случае при вычерчивании рамки будет затерта строка заголовка.
Рекомендуемая литература
Для ознакомления с общими концепциями объектно-ориентированных вычислений и их практической реализацией я бы рекомендовал статьи из сборника [Peterson, 1987]. Обзор работ по объектно-ориентированной технологии применительно к задачам искусственного интеллекта читатель найдет в [Stefik and Bobrow, 1986]. В работе [Кеепе, 1989] довольно подробно описан язык CLOS.
Подробное описание C++ и методики программирования на этом языке содержится в книгах [Booch, 1994] и [Meyers, 1995], [Meyers, 1997], хотя я и не в восторге от двух последних.
ориентированные языки программирования от обычных
1. Чем отличаются объектно- ориентированные языки программирования от обычных процедурных языков?
2. В чем состоит отличие между конкретными и абстрактными классами?
3. Почему при множественном наследовании иерархическая структура превращается в гетерархическую?
4. В чем состоит проблема наложения методов при множественном наследовании?
5. Что такое метакласс и в чем польза применения такой конструкции?
6. Что понимается под термином "список предшествования классов"? 7. Рассмотрите схему отношений между классами на рис. 7.9.
Используя конструкцию def class языка CLIPS, опишите эту структуру классов таким образом, чтобы соблюдался следующий порядок наследования в классах, имеющих несколько суперклассов:
wkg-man: (man worker) father: (parent man)
wkg-woman: (worker woman) mother: (parent woman)
wkg-father: (wkg-man father)
wkg-raother: (mother wrk-woman)
Начните с класса person:
(defclass person (is-a USER) (role concrete))
Какой вид будет иметь список предшествования классов wkg-father и wkg-mother?
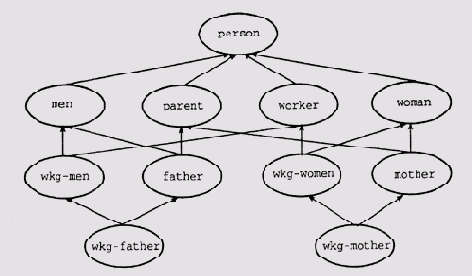
Рис. 7.9. Схема структуры классов для упражнения 7
8. Предположим, что классы на рис. 7.9 имеют следующие предпочтения при выборе блюд на завтрак:
man: donut woman:
croissant parent:
fruit worker: bacon
Закодируйте данные предпочтения в обработчиках сообщений этих классов таким образом, чтобы класс-получатель сообщения вернул наименование того блюда, которое он предпочитает.
Сформируйте следующие экземпляры классов:
Joan — экземпляр класса wrk-mother,
Jim — экземпляр класса wrk-man.
Передайте им сообщение, например, в такой форме:
(send [Joan] breakfast)
Чем ответят экземпляры Joan и Jim на такое сообщение и почему?
Формальные языки
Математическая логика является формальным языком в том смысле, что в отношении любой последовательности символов она позволяет сказать, удовлетворяет ли эта последовательность правилам конструирования выражений в этом языке (формулам). Обычно формальным языкам противопоставляются естественные, такие как французский и английский, в которых грамматические правила не являются жесткими. Утверждение, что логика является исчислением с определенными синтаксическими правилами логического вывода, означает, что влияние одних членов выражения на другие зависит только от формы выражения в данном языке и ни коим образом не зависит от каких-либо посторонних идей или интуитивных предположений.
Под автоматическим формированием суждений (automated reasoning) понимается поведение некоторой компьютерной программы, которая строит логический вывод на основании определенных законов. Так, нельзя отнести к классу программ автоматического формирования суждений программу, которая моделирует подбрасывание монетки, чтобы определить, следует ли одна формула из набора других. (В литературе также часто встречается термин автоматическая дедукция (automated deduction), равнозначный по смыслу термину автоматическое формирование суждений.)
При реализации автоматического формирования суждений, как правило, стремятся к максимально возможному единообразию и стандартизации в представлении формул, но в то же время в литературе часто приходится сталкиваться с самыми разнообразными системами обозначений, относящихся к логике. Основными синтаксическими схемами представления выражений являются конъюнктивная нормальная форма (conjunctive normal form— CNF), полная фразовая форма (full clausal form) и фраза Хорна (Horn clause), последняя является подмножеством полной фразовой формы. Далее мы увидим, что эти формы представления значительно упрощают процедуру логического вывода, но сначала рассмотрим некоторые вопросы исчисления высказываний и предикатов.
Исчисление предикатов
Исчисление высказываний имеет определенные ограничения. Оно не позволяет оперировать с обобщенными утверждениями вроде "Все люди смертны". Конечно, можно обозначить такое утверждение некоторой пропозициональной константой р, а другой константой q обозначить утверждение "Сократ — человек". Но из (р л q) нельзя вывести утверждение "Сократ смертен".
Для этого нужно анализировать пропозициональные символы в форме предикатов и аргументов, кванторов и квантифщированных переменных. Логика предикатов предоставляет нам набор синтаксических правил, позволяющих выполнить такой анализ, набор семантических правил, с помощью которых интерпретируются эти выражения, и теорию доказательств, которая позволяет вывести правильные формулы, используя синтаксические правила дедукции. Предикатами обозначаются свойства, такие как "быть человеком", и отношения, такие как быть "выше, чем".
Аргументы могут быть отдельными константами, или составным выражением "функция-аргумент", которое обозначает сущности некоторого мира интересующих нас объектов, или отдельными квантифицируемыми переменными, которые определены в этом пространстве объектов. Специальные операторы — кванторы — используются для связывания переменных и ограничения области их интерпретации. Стандартными являются кванторы общности (V) и существования (3). Первый интерпретируется как "все", а второй — "кое-кто" (или "кое-что").
Ниже приведены синтаксические правила исчисления предикатов первого порядка.
Любой символ (константа или переменная) является термом. Если rk является символом k-местной функции и а1 ..., <xk являются термами, то Гk(a1..., ak) является термом.
(S 40
Если Tk является символом k-местного предиката
и а1 ..., ak являются термами,
то U(а1 ..., ak) является правильно построенной формулой (ППФ).
(S. -) и (S. v)
Правила заимствуются из исчисления высказывании.
(S. V) Если U является ППФ и % является переменной,
то (любой Х) U является ППФ.
Для обозначения используются следующие символы:
U — произвольный предикат;
Г — произвольная функция;
a — произвольный терм;
X — произвольная переменная.
Действительные имена, символы функций и предикатов являются элементами языка первого порядка.
Использование квантора существования позволяет преобразовать термы с квантором общности в соответствии с определением
(EX)U определено как -(любой X)-U.
Выражение (EХ)(ФИЛОСОФ(Х)) читается как "Кое-кто является философом", а выражение (любой Х)(ФИЛОСОФ(Х)) читается как "Любой является философом". Выражение ФИЛОСОФ(Х) представляет собой правильно построенную формулу, но это не предложение, поскольку область интерпретации для переменной X не определена каким-либо квантором. Формулы, в которых все упомянутые переменные имеют определенные области интерпретации, называются замкнутыми формулами.
Как и в исчислении высказываний, в исчислении предикатов существует нормальная форма представления выражений, но для построения такой нормальной формы используется расширенный набор правил синтаксических преобразований. Ниже приведена последовательность применения таких правил. Для приведения любого выражения к нормальной форме следует выполнить следующие операции.
(1) Исключить операторы эквивалентности, а затем импликации.
(2) Используя правила Де Моргана и правила замещения (E X)U на -(любой X)-U (а следовательно, и (любой X) U на -(E X)-U), выполнить приведение отрицания.
(3) Выполнить приведение переменных. При этом следует учитывать особенности определения области интерпретации переменных кванторами. Например, в выражении (E Х)(ФИЛОСОФ(Х))&(E Х)(АТЛЕТ(Х)) переменные могут иметь разные интерпретации в одной и той же области. Поэтому вынесение квантора за скобки — (E Х)(ФИЛОСОФ(Х))&.(АТЛЕТ(Х))— даст выражение, которое не следует из исходной формулы.
(4) Исключить кванторы существования. Кванторы существования, которые появляются вне области интерпретации любого квантора общности, можно заменить произвольным именем (его называют константой Сколема), в то время как экзистенциальные переменные, которые могут существовать внутри области интерпретации одного или более кванторов общности, могут быть заменены функциями Сколема.
Функция Сколема— это функция с произвольным именем, которая имеет следующий смысл: "значение данной переменной есть некоторая функция от значений, присвоенных универсальным переменным, в области интерпретации которых она лежит".
(5) Преобразование в префиксную форму. На этом шаге все оставшиеся кванторы (останутся только кванторы общности) переносятся "в голову" выражения и таким образом оказываются слева в списке квантифицированных переменных. За ними следует матрица, в которой отсутствуют кванторы.
(6) Разнести операторы дизъюнкции и конъюнкции.
(7) Отбросить кванторы общности. Теперь все свободные переменные являются неявно универсально квантифицированными переменными. Экзистенциальные переменные станут либо константами, либо функциями универсальных переменных.
(8) Как и ранее, отбросить операторы конъюнкций, оставив множество фраз.
(9) Снова переименовать переменные, чтобы одни и те же имена не встречались в разных фразах.
8.1. Снова о роботах и комнатах
В главе 3 мы уже упоминали об исчислении предикатов в упрощенном виде. Там выражение вида
at(робот, комнатаА)
означало, что робот находится в комнате А. Термы робот и комнатаА в этом выражении представляли собой константы, которые описывали определенные реальные объекты. Но что будет означать выражение вида
at(X, комнатаА) ,
в котором х является переменной? Означает ли оно, что нечто находится в комнате А? Если это так, то говорят, что переменная имеет экзистенциальную подстановку (импорт). А может быть, выражение означает, что все объекты находятся в комнате А? В таком случае переменная имеет универсальную подстановку. Таким образом, отсутствие набора четких правил не позволяет однозначно интерпретировать приведенную формулу.
Перечисленные в этом разделе правила исчисления предикатов обеспечивают однозначную интерпретацию выражений, содержащих переменные.
В частности, фраза
at(X, комнатаА )<—at (X, ящик1) интерпретируется как
"для всех X X находится в комнате А, если X находится в ящике 1".
В этой фразе переменная имеет универсальную подстановку. Аналогично, фраза
at(X, комнатаА) <-интерпретируется как "для всех X X находится в комнате А". А вот фраза
<— at(X, комнатаА) интерпретируется как "для всех XX не находится в комнате А".
Иными словами, это не тот случай, когда некоторый объект X находится в комнате А и, следовательно, переменная имеет экзистенциальную подстановку.
Теперь можно преобразовать фразовую форму, в которой позитивные литералы сгруппированы слева от знака стрелки, а негативные — справа. Если фраза в форме
P1, ..., Рт <— q1,...qn содержит переменные х1,..., хk, то правильная интерпретация имеет следующий вид:
для всех x1, ..., хk
p1 или ... или pm является истинным, если q1 и ... и qn являются истинными.
Если п = 0, т.е. отсутствует хотя бы одно условие, то выражение будет интерпретироваться следующим образом:
для всех x1, ..., xk
p1 или ... или рт является истинным.
Если т = 0, т.е. отсутствуют термы заключения, то выражение будет интерпретироваться следующим образом:
для всех x1, ..., xk
не имеет значения, что q1 и ... и qn являются истинными.
Если же т = п = 0, то мы имеем дело с пустой фразой, которая всегда интерпретируется как ложная.
Исчисление высказываний
Исчисление высказываний представляет собой логику неанализируемых предположений, в которой пропозициональные константы могут рассматриваться как представляющие определенные простые выражения вроде "Сократ — мужчина" и "Сократ смертен". Строчные литеры р, q, r, ... в дальнейшем будут использоваться для обозначения пропозициональных констант, которые иногда называют атомарными формулами, или атомами.
Ниже приведены все синтаксические правила, которые используются для конструирования правильно построенных формул (ППФ) в исчислении высказываний.
(S. U) ЕслиU является атомом, то у является ППФ.
(S¬) Если U является ППФ, то —U также является ППФ.
(S. v) Если U и ф являются ППФ, то (U u ф) также является ППФ.
В этих правилах строчные буквы греческого алфавита (например, U и ф) представляют пропозициональные переменные, т.е. не атомарные формулы, а любое простое или составное высказывание. Пропозициональные константы являются частью языка высказываний, который используется для приложения исчисления пропозициональных переменных к конкретной проблеме.
Выражение -U читается как "не U", а (U v ф) читается как дизъюнкция "U или ф (или оба)". Можно ввести другие логические константы — "л" (конъюнкция), "D" (импликация, или обусловленность), "=" (эквивалентность, или равнозначность), которые, по существу, являются сокращениями комбинации трех приведенных выше констант. .
(U ^ ф) Эквивалентно¬(¬U v ф). Читается "U и ф".
(U

(U==ф) Эквивалентно (U


В конъюнктивной нормальной форме исчисления высказываний константы "импликация" и "эквивалентность" заменяются константами "отрицание" и "дизъюнкция", а затем отрицание сложного выражения раскрывается с помощью формул Де Моргана:
¬(U^ф) преобразуется в (¬Uv¬ф), ¬(U v ф) преобразуется в (-U^ф) , ¬¬U преобразуется в U .
Последний этап преобразований — внесение дизъюнкций внутрь скобок: (£ v (U ^ф))) заменяется ((£vU\(U)^(£vф)).
Принято сокращать вложенность скобочных форм, отбрасывая в нормальной конъюнктивной форме знаки операций v и л. Ниже представлен пример преобразования выражения, содержащего импликацию двух скобочных форм, в нормальную конъюнктивную форму.
¬(pvq)

¬¬(pvg)v(-p^- q) Исключение~.
(pvq)v(-p^- q) Ввод - внутрь скобок.
(¬pv(pvq))v(¬pv(pvq)) Занесение v внутрь скобок.
{{-p, р, q}, {¬q, р, q} } Отбрасывание А и v в конъюнктивной нормальной форме.
Выражения во внутренних скобках — это либо атомарные формулы, либо негативные атомарные формулы. Выражения такого типа называются литералами, причем с точки зрения формальной логики порядок литералов не имеет значения. Следовательно, для представления множества литералов — фразы — можно позаимствовать из теории множеств фигурные скобки. Литералы в одной и той же фразе неявно объединяются дизъюнкцией, а фразы, заключенные в фигурные скобки, неявно объединяются конъюнкцией.
Фразовая форма очень похожа на конъюнктивную нормальную форму, за исключением того, что позитивные и негативные литералы в каждой дизъюнкции группируются вместе по разные стороны от символа стрелки, а затем символ отрицания отбрасывается. Например, приведенное выше выражение
преобразуется в две фразы:
p,q<¬q.
в которых позитивные литералы сгруппированы слева от знака стрелки, а негативные справа.
Более строго, фраза представляет собой выражение вида
в котором p1..., рт q1,..., qn являются атомарными формулами, причем т=>0 и п=>0. Атомы в множестве р1,..., рт представляют заключения, объединенные операторами дизъюнкции, а атомы в множестве q1 ..., qn — условия, объединенные операторами конъюнкции.
Язык PROLOG
Фразы Хорна (Horn clause) представляют собой подмножество фраз, содержащих только один позитивный литерал. В общем виде фраза Хорна представляется выражением
В языке PROLOG эта же фраза записывается в таком виде (обратите внимание на символ точки в конце):
р :- q1,...,qn. Такая фраза интерпретируется следующим образом:
"Для всех значений переменных в фразе p истинно, если истинны q1 и ... и qn",
т.е. пара символов ":-" читается как "если", а запятые читаются как "и".
PROLOG — это не совсем обычный язык программирования, в котором программа состоит в основном из логических формул, а процесс выполнения программы представляет собой доказательство теоремы определенного вида.
Фраза в форме
р :- q1, ...,qn.
может рассматриваться в качестве процедуры. Такая процедура предполагает следующий порядок выполнения операций.
(1) Литерал цели сопоставляется с литералом р (унифицируется с р), который называется головой фразы.
(2)Хвост фразы ql, ...,qn конкретизируется подстановкой значений переменных (или унификаторов), сформированных в результате этого сопоставления.
(3) Конкретизированные термы хвостовой части образуют затем множество подцелей, которые могут быть использованы другими процедурами.
Таким образом, сопоставление (или унификация) играет ту же роль, что и передача параметров функции в других, более привычных языках программирования.
Например, рассмотрим набор фраз языка PROLOG, представленных в листинге 8.1. Предположим, что a, b и с — какие-то блоки в мире блоков. Две первые фразы утверждают, что а находится на (on) b, a b находится на (on) с. Третья фраза утверждает, что X находится выше (above) Y, если X находится на (on) Y. Четвертая фраза утверждает, что X находится выше (above) Y, если существует какой-то другой блок Z, размещенный на (on) Y, и X находится выше (above) Y.
Листинг 8.1. Простая программа на языке PROLOG, определяющая отношение on (на)
on(а, b).
on(b, с).
above(X, Y) :- on(X, Y).
above(X, Y) :- on(Z, Y),
above(X, Z).
Очевидно, что от программы требуется вывести цель above (а, с) из этого множества фраз. Как это делается, мы увидим в разделе 8.3.2, но уже сейчас можно сказать, что процесс формулировки выражения цели включает обработку двух процедур above и использование двух фраз on.
Логическое программирование
8.1. Формальные языки
8.2. Язык PROLOG
8.3. Опровержение резолюций
8.4. Процедурная дедукция в системе PLANNER
8.5. PROLOG и MBASE
Рекомендуемая литература
Упражнения
Еще в конце 1970-х годов стала отчетливо просматриваться тенденция к использованию в исследованиях в области искусственного интеллекта "формальных" методов, т.е. основанных на аппарате математической логики. Эти методы противопоставлялись более интуитивным и менее формализованным эвристическим методам, скажем, таким, которые были использованы в системе MYCIN. Для того чтобы стало ясно, что все это значит, нужно познакомить вас с логическими языками, а затем показать, как соотносятся их свойства с теми методами рассуждений, которые должны поддерживать типовые экспертные системы.
Опровержение резолюций
В языке PROLOG используется "интерпретация фраз Хорна для решения проблем" (см. [Kowalski, 1979, р. 88-89]). Фундаментальный метод доказательства теорем, на котором базируется PROLOG, называется опровержением резолюций (resolution refutation). Полное описание этого метода читатель найдет в книге Робинсона [Robinson, 1979], а в этом разделе мы попытаемся кратко изложить только основные идеи.
Поиск доказательствв системе резолюций
Резолюция представляет собой правило вывода, с помощью которого можно вывести новую ППФ (правильно построенную формулу) из старой. Однако в приведенном выше описании логической системы ничего не говорилось о том, как выполнить доказательство. В этом разделе мы обратим основное внимание на стратегические аспекты доказательства теорем.
Пусть р представляет утверждение "Сократ — это человек", a q — утверждение "Сократ смертен". Пусть наша теория имеет вид
Т={{¬р,q}, {р}}.
Таким образом, утверждается, что если Сократ человек, то Сократ смертен, и что Сократ — человек. {17} выводится из теории Т за один шаг резолюции, эквивалентной правилу modus ponens. .
Выражения {¬р, q} и {р} "сталкиваются" на паре дополняющих литералов р и ¬р, а {q} является резольвентой. Таким образом, теория Алогически подразумевает д, что записывается в форме Т|-q. Теперь можно добавить новую фразу {q} — резольвенту — в теорию Т и получить таким образом теорию
Т'= {{ ¬ip, q}, {p}, {q}}.
Конечно, в большинстве случаев для доказательства требуется множество шагов. Положим, например, что теория Т имеет вид
В этой теории р и q сохраняют прежний смысл, а г представляет утверждение "Сократ — бог". Для того чтобы показать, что Т|- ¬r , потребуются два шага резолюции:
{¬q,p},{Р}/{q}
{¬q,-r},{q} / {-r}
Обратите внимание, что на первом шаге используются две фразы из исходного множества Т, а на втором— резольвента {q}, добавленная к Т. Кроме того, следует отметить, что доказательство может быть выполнено и по-другому, например:
{¬p,q},{¬q,¬r}/{¬p,¬r},
{¬p,¬r},{p}/{¬r}
При таком способе доказательства к Т добавляется другая резольвента. В связи со сказанным возникает ряд проблем.
Когда множество Т велико, естественно предположить, что должно существовать несколько способов вывести интересующую нас конкретную формулу (эта формула является целевой). Естественно, что предпочтение следует отдать тому методу, который позволяет быстрее сформулировать доказательство.
Множество Т может поддерживать и те правила, которые не имеют ничего общего с доказательством целевой формулы. Как же заранее узнать, какие правила приведут нас к цели?
Потенциально весь процесс подвержен опасности комбинаторного взрыва. На каждом шаге множество Г растет, и в нашем распоряжении оказывается все больше и больше возможных путей продолжения процесса, причем некоторые из них могут привести в зацикливанию.
Та схема логического вывода, которой мы следовали до сих пор, обычно называется прямой, или восходящей стратегией. Мы начинаем с того, что нам известно, и строим логические суждения в направлении к тому, что пытаемся доказать. Один из возможных способов преодоления сформулированных выше проблем — попытаться действовать в обратном направлении: от сформулированной целевой формулы к фактам, которые нужны нам для доказательства истинности этой формулы.
Предположим, перед нами стоит задача вывести {q} из некоторого множества фраз
Т= {...,{ ¬p, q},...}.
Создается впечатление, что это множество нужно преобразовать, отыскивая фразы, включающие q в качестве литерала, а затем попытаться устранить другие литералы, если таковые найдутся. Но фраза {q} не "сталкивается" с такой фразой, как, например, { —р, q}, поскольку пара, состоящая из одинаковых литералов q, не является взаимно дополняющей.
Если q является целью, то метод опровержения резолюции реализуется добавлением негативной формулы цели к множеству Т, а затем нужно показать, что формула
Т' = Т U {¬q}
является несовместной. Полагая, что множество Т непротиворечиво, приходим к выводу, что Т' может быть противоречивым вследствие Т |- q.
Рассмотрим этот вопрос более подробно. Сначала к существующему множеству фраз добавляется отрицание проверяемой фразы {-q}. Затем предпринимается попытка резольвиро-вать {-q} с другой фразой в Т. При этом существуют только три возможные ситуации.
В Т не существует фразы, содержащей q. В этом случае доказать искомое невозможно.
Множество Т содержит {q}. В этом случае доказательство выполняется немедленно, поскольку из {¬q} и {q} можно вывести пустую фразу, что означает несовместность (наличие противоречия).
Множество Т содержит фразу {..., q, ...}. Резольвирование этой фразы с {¬q} формирует новую фразу, которая содержит остальные литералы, причем для доказательства противоречия все они должны быть удалены в процессе резольвирования.
Эти оставшиеся литералы можно рассматривать в качестве подцелей, которые должны быть разрешены, если требуется достичь главной цели. Описанная стратегия получила название нисходящей (или обратной) и очень напоминает формулирование подцелей в системе MYCIN.
В качестве примера положим, что множество Т, как и ранее, имеет вид {{¬p,q},{¬q,¬r},{p}}. Мы пытаемся показать, что Т|- ¬r. Для этого докажем, что фраза {r} является следствием существующего множества Т, для чего добавим к этому множеству отрицание фразы ¬r. Поиск противоречия происходит следующим образом:
[{¬q,¬r},{r}]/{¬q}
[{¬p,q},{¬q}]/{¬q}
[{¬p},{p}]/{}
Этот метод доказ_ательства теорем получил название "опровержение резолюции", поскольку, во-первых, он использует правило вывода резолюций, а во-вторых, следует стратегии "от противного" (стратегии опровержения).
Теперь вернемся к примеру PROLOG-программы, представленному в листинге 8.1. На рис. 8.1 показано дерево доказательства утверждения above(a, с). Дерево строится сверху вниз, и каждая ветвь связывает две "родительские фразы", в которых содержатся дополняющие литералы, с фразой, которая образуется в результате применения правила резолюции. Ко всем целям, записанным справа от значка ":-", неявно применяется отрицание. В левой части дерева представлены формулы целей, а в правой — фразы, взятые из базы данных.
Корнем дерева является пустая фраза {}. Это означает, что поиск доказательства был успешным. Добавление негативной фразы :- above (а, с) к исходному множеству (теории) привело к противоречию. Таким образом, можно утверждать, что фраза above (а, с) является логическим следствием из этой теории.
Обратите внимание на роль операции унификации в этом доказательстве.
Цель above (а, с) унифицируется с головной фразой above(X, Y) с помощью подстановки {Х/а, Y/c}, где выражение Х/а можно интерпретировать как "X получает значение а". Затем эта подстановка применяется к хвостовой части фразы
on(Z, Y), above(X, Z),
из чего следует формулировка подцелей
on(Z, с), above(a, Z).
Следующая подцель on(Z, с) унифицируется с on(b, с) подстановкой {Z/b}. Эта подстановка затем применяется и к оставшейся подцели, которая таким образом превращается в above (а, b), и так до тех пор, пока не образуется пустая фраза.
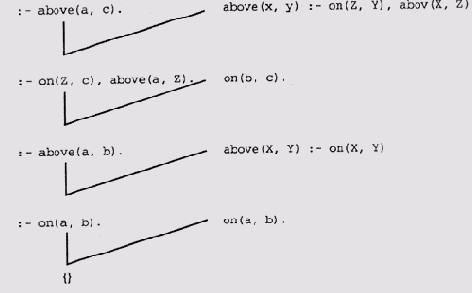
Рис. 8.1. Дерево доказательства методом опровержения резолюций
Восходящий процесс доказательства, использующий в качестве отправной точки утверждение, которое мы стараемся доказать, позволяет сфокусировать внимание на процессе поиска решения, поскольку анализируемые логические связи по крайней мере потенциально ведут нас к цели. Правда, основанный на этой стратегии метод опровержения резолюций не позволяет решить все перечисленные выше проблемы. В частности, этот метод не гарантирует, что найденный путь доказательства будет короче других (или длиннее).
В следующих двух разделах мы рассмотрим эволюцию процедурных дедуктивных систем, т.е. систем, в которых процедуры используются для добавления дополнительных управляющих свойств в процесс целенаправленного поиска и для представления знаний, которые не имеют четко выраженного декларативного характера.
Процесс становления этого класса систем весьма поучителен, поскольку демонстрирует, как, отталкиваясь от стандартной логики и добавляя методики, обычно используемые при доказательстве теорем, можно построить успешно функционирующую автоматическую систему доказательства.
Правилпоискв языке PROLOG
Существует аналогия между выражениями вида
admire(Y, X) :- philosopher (X) , beats (X,Y)
в языке PROLOG и консеквентной теоремой в системе PLANNER. При запросе "who admires whom?" ("кто кем восхищается?"), который может быть представлен в виде фразы
:- admire(V, W). ,
приведенное выше выражение интерпретируется следующим образом: "Для того чтобы показать, что Y восхищается X, покажите, что X является философом, а затем покажите, что X обогнал Y".
Цель, которая унифицируется с выражением admire(Y, X), может быть истолкована как вызов процедуры, а процесс унификации может рассматриваться как механизм передачи действительных параметров другим литералам, образующим тело процедуры. В данном случае не имеет значения, являются ли эти "параметры" переменными, как в представленном примере. Подцели в теле процедуры упорядочены. В языке PROLOG такое упорядочение называется правилом поиска слева направо.
В PLANNER и ранних системах, основанных на методе резолюций, цель легко достигается, если в базе данных содержатся утверждения
philosopher (zeno) . beats (zeno, achilles).
Тогда получим ответ
admire (achilles, zeno).
Если в базе данных содержится другая информация, касающаяся искомой цели, то программе может потребоваться выполнить обратный просмотр (backtrack), прежде чем добраться до цели. Обратный просмотр используется в том случае, когда нужно отменить присвоение значений переменным, выполненное при обработке некоторой подцели, поскольку это присвоение приводит к неудаче в обработке поздней подцели. Положим, что база данных содержит дополнительную фразу
philosopher ( socrates ) .
В этом случае, если эта формула отыщется прежде, чем формула
philosopher(zeno).,
обработка следующей подцели приведет к неудаче, а следовательно, нужно будет поискать другого философа. Объем работы, который придется выполнить системе в процессе достижения цели admire(V, W), зависит от количества альтернативных вариантов утверждений, касающихся философов, которые имеются в базе данных.
Предположим, что в базе данных содержатся факты еще о ста философах, т.е. в ней имеются сто других выражений в формате philosopher(X), в которых X отличается от zeno. Тогда в худшем случае программе потребуется 100 раз выполнить обратный просмотр, прежде чем будет найдено именно то утверждение, которое согласуется с целью.
База данных может содержать и другие правила, которые взаимодействуют с интересующим нас выражением admire (V, W). Например, можно положить, что утверждение "X обогнал Y" представляет транзитивное отношение. В этом случае в нашем распоряжении будет правило
beats(X, Y) :- beats(X, Z), beatsf Z, Y).
Можно также дать такое определение понятию "философ", что таковым будет считаться только тот, кого хотя бы однажды обогнала черепаха:
philosopher(X) :- beats(Y, X), tortoise(Y).
Наличие этих правил очень усложнит пространство поиска и значительно увеличит количество случаев, когда придется выполнять обратный просмотр.
В следующем разделе описано одно из расширений языка PROLOG— система MBASE, на базе которой реализована программа МЕСНО для решения задач вузовского курса теоретической механики.
Принцип резолюций
8.3.1. Принцип резолюций
Ранее я уже вскользь упоминал о том, что мы стараемся упростить синтаксис исчисления таким образом, чтобы уменьшить количество правил влияния, необходимое для доказательства теорем. Вместо дюжины.или более правил, которые используются при доказательстве теорем вручную, системы автоматического доказательства для фразовых форм используют единственное правило вывода — принцип резолюций, — впервые описанное Робинсоном ([Robinson, 1965]).
Рассмотрим следующий пример из исчисления высказываний. В дальнейшем прописными буквами Р, Q, R,... будут обозначаться отдельные фразы, а строчными греческими U, ф и £ — пропозициональные переменные, как и раньше.
Если U и ф представляют две произвольные фразы, которые можно представить в конъюнктивной нормальной форме, и
U={ U1, ..., Ui, ...., Um},
и
ф= {ф1..., фi.....,фn}, и
Ui, = ¬фi при 1[i[mm,1 [j [ n,
то новую фразу £ можно вывести из объединения U' и ф', где
U' = U¬{ Ui} и ф' = ф¬{ф,}.
Фраза £ = U' и ф' называется резольвентой шага резолюции, а U и ф являются родительскими фразами. Иногда говорят, что U и ф "сталкиваются" на паре дополняющих литералов Ui , и фj.
Мощность резолюции обеспечивается тем, что в ней суммируется множество других правил. Это станет очевидно после того, как обычные правила будут представлены в конъюнктивной нормальной форме.
В левой колонке табл. 8.1 перечислены наименования правил вывода, в средней показано, как они выглядят в обычных обозначениях, а в правой колонке — во фразовой форме. В каждой записи выражения в верхней части представляют схему предпосылок, а выражения в нижней части — схему заключений. Из этой таблицы видно, что каждое из цитированных выше пяти правил является одним из экземпляров резолюции!
Таблица 8.1. Обобщение резолюции
|
Правило вывода |
Обычная форма |
Конъюнктивная нормальная форма | |||||
|
Modus ponens |
(U  |
{¬U,Ф},{U}/{ф} | |||||
|
Modus fallens |
(U  |
{¬U,ф},{-,ф}/{-U} | |||||
|
Сцепление |
(U    |
{¬U,ф},{¬ф,£}/{¬U,£} | |||||
|
Слияние |
(U   |
{U,ф},{¬U,ф}/{ф} | |||||
|
Reductio |
(U,¬U)/ | |
{¬U},{U}/{} |
Обратите внимание на то, что противоречие в правиле, которое обычно обозначается значком 1, дает в результате пустую фразу— {}. Это означает, что предпосылки несовместимы. Если считать, что предпосылки описывают некоторое состояние предметной области, то такой набор предпосылок не может быть реально обеспечен в ней, т.е. такое состояние невозможно.
Главное, что нужно вынести из всего сказанного выше, что компонент автоматического доказательства теорем, который является основным компонентом большинства систем искусственного интеллекта и, в частности, языков программирования искусственного интеллекта, таких как PROLOG, является системой, опровержения резолюций. Для того чтобы доказать, что р следует из некоторого описания состояния (или теории) Т, нужно положить —р и попытаться доказать, что из этого предположения следует утверждение, противоречащее Т. Если это удастся сделать, то тем самым подтверждается утверждение р, а в противном случае оно опровергается.
В исчислении предикатов использование резолюций требует дополнительных усилий, поскольку в этом исчислении присутствуют переменные. Основная операция сопоставления в доказательстве теорем с помощью резолюций называется унификацией (подробное описание используемого при этом алгоритма читатель найдет, например, в работе Нильсона [Nilsson, 1980]). При сопоставлении дополняющих литералов отыскивается такая подстановка переменных, которая превращает оба выражения в идентичные.
Например, выражения БЕЖИТ_БЫСТРЕЕ_ЧЕМ(Х, улитка) и БЕЖИТ_БЫСТРЕЕ _ЧЕМ (черепаха, Y) превращаются в идентичные при подстановке {Х/черепаха, Y/улитка}. Такая подстановка называется унификатором. Наша цель — отыскать наиболее общую подстановку такого рода.
Процедурная дедукция в системе PLANNER
Система PLANNER явилась одной из первых попыток разработки языка программирования задач искусственного интеллекта, базирующегося на идеях автоматического доказательства теорем. Хотя разработчикам и не удалось в полной мере реализовать задуманное, созданное подмножество языка, получившего название Micro-PLANNER, нашло применение в системах планирования, в частности в программе SHRDLU, представленной в главе 2. Ниже мы обсудим те аспекты системы PLANNER, которые имеют отношение к представлению знаний.
Система PLANNER моделировала состояние некоторой области рассуждений в терминах ассоциативной базы данных, которая содержала как утверждения, так и теоремы, функционирующие как процедуры. Утверждения представляли собой списки типа "предикат-аргумент", подобные тем, что используются в LISP. Например:
(BLOCK B1) (ON Bl TABLE)
Теоремы же в действительности представляли собой выражения, в которых можно было проследить влияние одних термов на другие. Например, теорема
(ANTE (BLOCK X) (ASSERT (ON X TABLE)))
в действительности является процедурой, которая говорит: "Если утверждается, что X это блок, то также утверждается, что X находится на столе". Таким образом, если существует утверждение (BLOCK B1), то можно также считать утверждением и выражение (ON Bl TABLE). Функция ASSERT добавляет собственный конкретизированный аргумент (т.е. аргумент, которому присвоено определенное значение) в базу данных.
Выше был приведен пример антецедентной теоремы. Это название акцентирует внимание на том, что нас интересует только логическая связь между антецедентом и консек-вентом (по аналогии с правилом modus ponens), а не связь между отрицанием консеквен-та и отрицанием антецедента (по аналогии с правилом modus fallens). Мы говорим, что в действительности эта теорема является процедурой, поскольку в ней содержится управляющая информация. Ее функционирование во многом напоминает демонов в системе фреймов, описанных в главе 6.
Система PLANNER поддерживает и другой вид процедур, которые получили наименование консеквентной теоремы. Пример процедуры такого типа приведен ниже:
(CONSE (MORTAL X) (GOAL (MAN X))).
Эта процедура может быть прочитана так: "Для того чтобы показать, что X смертен, покажите, что X — человек". Если выражение, которое нужно доказать (цель), сформулировано в виде (MORTAL SOCRATES) (Сократ смертен), то в качестве подцели будет выступать выражение (MAN SOCRATES) (Сократ человек). Функция GOAL организует поиск в базе данных собственного конкретизированного аргумента. Однако не удастся использовать эту теорему для перехода от утверждения (MAN SOCRATES) (Сократ человек) к утверждению (MORTAL SOCRATES) (Сократ смертен).
Консеквентные теоремы могут также манипулировать базой данных. Например, для того чтобы положить блок В1, на котором ничего не стоит, на блок В2, на котором также ничего не стоит, нужно отыскать, на чем же стоит блок В1, удалить соответствующее утверждение и сформировать новое, которое говорит, что блок В1 стоит на блоке В2.
(CONSE (ON X Y)
(GOAL (CLEAR X)) (GOAL (CLEAR Y))
(ERASE (ON X Z)) (ASSERT (ON X Y)))
Задавшись целью (ON Bl B2), если на Bl и на В2 ничего не стоит, PLANNER выполнит необходимые операции с базой данных. Таким образом, консеквентная теорема поддерживает в системах автоматизации планирования работу механизма реализации операторов, подобных тем, которые мы видели в программе STRIPS (см. главу 3).
Из этого краткого описания читатель может сделать заключение, что в системе PLANNER управляющая информация явно представлена в базе данных процедур, а не скрывается в компоненте, ведающем стратегией выполнения доказательства теорем, как это делается в системах, работающих на основе метода опровержения резолюций. Достоинство такого подхода состоит в том, что можно решить в каждом конкретном случае, какие правила влияния следует применять. Кроме того, в нашем распоряжении оказывается довольно эффективный инструмент моделирования изменения состояния задачи.
С концепцией процедурной дедукции связана проблема полноты. Система доказательства является полной, если все тавтологии, т.е.
тривиально истинные выражения вроде (р v —pi), могут быть выведены в ней как теоремы. В системе PLANNER это свойство отсутствует. Мы уже обращали внимание на то, что нельзя сформировать выражение (MORTAL SOCRATES) из базы данных, в которой содержатся
(MAN SOCRATES)
(CONSE (MORTAL X)
(GOAL (MAN X))).
Это те издержки, с которыми нужно смириться, если мы хотим объединить управляющую информацию с пропозициональным представлением. К сожалению, система PLANNER оказалась не более эффективной, чем системы, основанные на теоремах резолюций. Это произошло потому, что использованная в ней управляющая информация страдает "близорукостью", отсутствует общая стратегия, а имеющийся набор теорем позволяет формулировать локальные решения, которые могут давать, а могут и не давать желаемый эффект. Отсутствует в PLANNER и возможность каким-то образом формировать суждения о механизме управления, что-то вроде метаправил, о которых шла речь в главе 5.
В следующем разделе мы кратко остановимся на системах, в которых была предпринята попытка устранить эти недостатки.
PROLOG и MBASE
Ранее мы уже видели, что фразу, содержащую предположение, можно представить с помощью исчисления предикатов первого порядка. Фраза
"Если философ выиграет у кого-нибудь в забеге, то этот человек будет им восхищен" в формализме предикатов приобретет вид формулы
(любой A) (любой Y)(PHILOSOPHER(X)^BEATS(X, Y)

Эту формулу можно представить в конъюнктивной нормальной форме следующим образом:
{ADMIRE(Y, X), -ВЕАТS(Х, Y), ->PHILOSOPHER(X)}.
Также было показано, что если записать это выражение таким образом, чтобы слева от оператора ":-" стоял единственный позитивный литерал, а справа — негативные литералы, то получится выражение, представляющее фразу Хорна в синтаксисе языка логического программирования PROLOG:
admire (Y, X) :- philosopher ( X) , beats (X,Y).
Ниже мы рассмотрим, как организовать управление применением таких правил.
Рекомендуемая литература
Четкое изложение основных концепций теории доказательств в математической логике читатель найдет в работе Эндрюса [Andrews, 1986]. Я также рекомендую познакомиться с книгой [Quine, 1979] — переизданием классического труда, опубликованного впервые еще в 1940 году. Достаточно обширное введение в проблематику автоматического формирования суждений содержится в книге Робинсона [Robinson, 1979].
Более популярное изложение этого материала с упором на проблематику искусственного интеллекта можно найти в работе [Genesereth andNilsson, 1987, Chapters 1-5]. Обсуждение проблем математической логики в контексте искусственного интеллекта содержится в статье Хейеса и Мичи [Hayes and Michie, 1984]. Новой работой в этой области является книга Гинзберга [Ginsberg, 1993].
Управление поиском в системе MBASE
Один из распространенных способов управления поиском в применении к доказательству какого-либо утверждения — тщательное упорядочение базы данных. При поиске нужных фактов или правил исполнительная система языка PROLOG просматривает базу данных от начала до конца. Используя это обстоятельство, можно несколько сократить время доказательства.
Определенные факты (основные атомы — ground atoms) нужно разместить в базе данных раньше, чем правила, которые в качестве цели имеют соответствующие предикаты. Таким образом будут минимизированы издержки обращения к правилам. Например, утверждение
beats(achilles, zeno).
должно стоять раньше правила
beats(X, Y) :- beats(X, Z), beats( Z, Y).
Исключения из общих правил также должны располагаться в базе данных раньше, чем сами общие правила. Например, правило, утверждающее, что пингвины не летают,
flies(X) :- penguin(X), !, fail .
должно стоять раньше общего правила, гласящего, что птицы летают,
flies(X) :- bird(X).
Литерал fail представляет собой один из способов выражения отрицания в языке PROLOG. Кроме того, в языке PROLOG имеется литерал !, который называется "отсечением". Этот литерал говорит исполнительной системе PROLOG, что не нужно осуществлять возврат из этой точки. Комбинация литералов представляет эффективный механизм управления обратным просмотром, предотвращая выполнение ненужных операций.
Предположения по умолчанию реализуются включением неосновных атомов в самый конец базы знаний. Например, если желательно, чтобы по умолчанию квакеры считались пацифистами, то фраза
pacifist(X) :- quaker(X).
должна появиться после всех фраз вида
pacifist(nixon) :- !, fail.
В случае, если при просмотре базы знаний не будет найдено утверждение об обратном, касающееся конкретного квакера, то на него распространится утверждение, справедливое для всех остальных.
Общее правило гласит, что сначала в базе данных следует располагать данные об особых случаях, т.е. определенные факты и исключения, затем данные об общих случаях, например правила влияния, и последними должны располагаться сведения о свойствах по умолчанию.
Все эти требования соблюдены в системе MBASE, но, кроме того, еще существует и возможность управления глубиной поиска. В этой системе существуют литералы, задающие один из трех имеющихся режимов поиска.
Обращение к базе данных (DBC — database call). Этот режим ограничивает зону поиска только основными литералами в базе данных и таким образом исключает применение правил. Для настройки этого режима нужно включить основной литерал в предикат ВВС. Например, факт, что b1 является блоком, будет представлен фразой
DBC(block(b1)).
Тогда для некоторой фразы Р при обработке подцелей в форме DBC (Р) будет просматриваться только указанная часть базы данных.
Описанная выше комбинация литералов отсечения и неудачи также может использоваться в сочетании с предикатом DBC. Таким образом, формируется своего рода "ловушка", прекращающая поиск цели, которая не может быть найдена. Например, можно таким способом прекратить попытки доказать, что блок одновременно находится в двух местах:
at(Block, Placel) :-
DEC(at(Block, Place2)), different(Placel, Place2), !, fail.
Обратите внимание на то, что если бы в теле процедуры отсутствовал предикат ВВС, то программа очень быстро зациклилась.
Вызов правил влияния (DBINF — inference call) — это обычный режим работы исполнительной системы PROLOG с использованием всех имеющихся правил. При этом соблюдаются соглашения о порядке поиска в базе сверху вниз, а в правиле слева направо.
Порождающий вызов (СС — creative call). В этом режиме формируются место-держатели для неизвестных и выполняются вычисления в тех случаях, когда обычный режим может привести к неудаче. Режим используется для математических вычислений, когда отсутствуют значения всех переменных в уравнении.
С помощью литералов 1 и fail обычно определяется отрицание определенной процедуры, например, так:
not(P) :- call(P) !, fail. not(P) .
В языке PROLOG специальный предикат call обрабатывает цель, переданную ему в качестве параметра. Идея состоит в том, что если такая обработка приведет к успеху, то отрицание цели приведет к неудаче, а литерал отсечения предотвратит обратный просмотр.
В противном случае мы перейдем ко второй фразе, и отрицание цели очевидно приведет к успеху.
Некоторые из проблем полноты, отмеченные в системе PLANNER, существуют и в языке PROLOG. В частности, использование литералов отсечения и неудачи может серьезно сказаться на полноте и согласованности фактов и правил. Существует множество способов внедрения отрицаний в логику фразы Хорна, но условия, при которых это можно сделать, весьма ограничены (см., например, [Shepherdson, 1984], [Shepherdson, 1985]).
Тем не менее исследователи пришли к выводу, что описанный выше механизм управления далеко не всегда может привести процесс вычислений к искомому заключению, поскольку не обладает достаточной "глобальностью". Проблема состоит в том, что все описанные методы базируются все-таки на довольно ограниченных, локальных знаниях о текущем состоянии процесса вычислений. В MBASE была предпринята попытка дополнить локальное управление двумя механизмами— схематизацией (schemata) и мета-предикатами. О них-то и пойдет речь ниже.
Под схематизацией подразумеваются ассоциативные механизмы, которые используются в основном для представления в компьютере знаний общего характера. Например, ниже приведено представление знаний о системе подъема грузов на основе ворота (pulley system):
sysinfo(pullsys,
[Pull, Str, P1, P2],
[pulley, string, solid, solid]
[ supports(Pull, Str),
attached(Str, Pi),
attached(Str, P2) ]).
Предикат sysinfo принимает четыре аргумента, каждый из которых аналогичен слоту в системе фреймов (см. об этом в главе 6):
первый аргумент, pullsys, свидетельствует о том, что эта схема представляет типовую систему подъема грузов с воротом и, таким образом, аналогичен слоту наименования;
второй аргумент, [Pull, Str, P1, P2], является перечнем деталей в этом механизме — ворот, трос и два груза;
третий аргумент, [pulley, string, solid, solid], содержит информацию о типе этих компонентов;
четвертый аргумент содержит список отношений (связей) между компонентами.
Обратите внимание на то, что в этом представлении нет никакой пропозиционально-сти, например сведений о том, каким способом можно неявно сопоставить два списка. По существу, это представление очень похоже на описание фрейма (но вряд ли с ним можно работать так же эффективно).
Описанная схематизация представляет только один из использованных в МЕСНО способов организации фоновой информации, которая нужна программе. Имеются и другие типы структур, которые помогают выбрать подходящие формулы для определения характеристических параметров той или иной моделируемой системы. Например, выражение
kind(al, accel, relaccel(...)).
означает, что al является параметром типа accel (ускорение), который определен в утверждении relaccel, т.е. в контексте относительных ускорений. Другое выражение
relates(accel, [resolve, constaccel, relaccel)).
означает, что формулы resolve, constaccel и relaccel содержат переменные типа accel и, следовательно, могут быть использованы для вычисления ускорения. Приведенные выражения можно рассматривать как один из видов дополнительного индексирования в ассоциативной сети. В данном случае индексирование представлено в форме логики, причем используются структуры, обычно редко встречающиеся в исчислении предикатов первого порядка.
Роль метапредикатов состоит в отборе правил, наиболее подходящих для вывода конкретной цели. Рассмотрим следующий пример:
solve(U, Exprl, Ans) :-
occur)U, Exprl, 2), collect(U, Exprl, Expr2), isolate(U, Expr2, Ans).
Эта процедура означает, что Ans является уравнением, которое решается относительно неизвестного U в выражении Exprl, если
в выражение Exprl неизвестная U входит дважды:
выражение Ехрг2 представляет собой Exprl, в котором выполнено приведение неизвестной U;
Ans является выражением Ехрг2, в котором неизвестная U вынесена в левую часть.
В данном случае метапредикат solve указывает способ преобразования уравнения к виду, который позволит разрешить его относительно неизвестного. Метапредикаты используются для того, чтобы формировать суждения о том, как формировать суждения, и в этом подобны метаправилам в продукционных системах.
Некоторые примеры использования системы МЕСНО демонстрируют, что методика логического программирования во многом сходна с программированием на обычных языках. Однако при создании приложений, которые требуют обработки обширного набора структурированных фактов, подчиняющихся определенным физическим законам (анализ электрических цепей или сложных механических систем), единственным подходящим языком часто оказывается PROLOG. Этот же язык может быть использован и для описания теорий, затрагивающих такие общие категории, как пространство, время, допустимость и обязательность, в которых существуют общие принципы, допускающие декларативное представление, и в которых не требуется глубокий поиск.
В главе 23 мы увидим, что, несмотря на существование определенных проблем при использовании концепций логического программирования и основанного на них языка PROLOG, эта концепция имеет приложение в двух других областях исследований, которые представляют интерес с точки зрения экспертных систем, а именно: обобщение на базе объяснения (explanation-based generalization) и логический вывод на метауровне (meta-level inference). Обобщение на базе объяснения используется для машинного обучения, а логический вывод на метауровне позволяет программе строить суждения о собственном поведении.
с помощью логики предикатов следующие
1. Выразите с помощью логики предикатов следующие утверждения.
I) Каждый студент использует какой-нибудь компьютер, и по крайней мере один компьютер используется каждым студентом. (Используйте только предикаты СТУДЕНТ, КОМПЬЮТЕР и ИСПОЛЬЗУЕТ.)
II) Каждый год некоторые студенты-мужчины проваливают каждый экзамен, но каждый студент-женщина сдает какой-нибудь экзамен. (Используйте только предикаты СТУДЕНТ, МУЖЧИНА, ЖЕНЩИНА, СДАЕТ, ЭКЗАМЕН, ГОД.)
Ill) Каждый мужчина любит какую-нибудь женщину, которая любит другого мужчину. (Используйте только предикаты МУЖЧИНА, ЖЕНЩИНА, ЛЮБИТ и = .)
IV) Не существует двух философов, которые любили бы одну и ту же книгу. (Используйте только предикаты ФИЛОСОФ, КНИГА, ЛЮБИТ и = .)
2. Выразите предложения упр. 1 в форме фразы.
3. Имеет ли смысл выразить следующие цитаты с помощью логики предикатов? Покажите, в чем состоит сложность такого преобразования в каждом конкретном случае.
I) Ни один человек не является островом. (Джон Донн (John Donne))
II) Человек, который живет где-нибудь, живет везде. (Тацит)
III) Прошлое — это иная страна. В нем все происходит по-другому. (Л. П. Хартли (L. P. Hartley))
4. Следующая формула утверждает, что кто-то бреет себя сам или парикмахер бреет кого-то:
бреет) X, X), бреет (парикмахер, X) <—
I) Используя обратную стратегию, покажите, что из этой формулы следует
бреет (парикмахер, парикмахер) <-
II) То же самое покажите с помощью прямой стратегии.
III) Как вы понимаете в том же контексте следующую фразу:
<- бреет(У, Y), бреет (парикмахер, У)
IV) Покажите, что следующие фразы противоречивы. Для этого достаточно показать, что из них следует пустая фраза:
бреет(Х, X), бреет (парикмахер, X)
<-<- бреет(У, Y), бреет (парикмахер, Y)
5. Ниже представлены правило поиска неисправности и описание конкретной ситуации.
Если компьютер не включается и напряжение в сети питания в норме, то оборван шнур питания или неисправен блок питания. Мой компьютер не включается.
Источники неопределенности
При решении проблем мы часто встречаемся со множеством источников неопределенности используемой информации, но в большинстве случаев их можно разделить на две категории: недостаточно полное знание предметной области и недостаточная информация о конкретной ситуации.
Теория предметной области (т.е. наши знания об этой области) может быть неясной или неполной: в ней могут использоваться недостаточно четко сформулированные концепции или недостаточно изученные явления. Например, в диагностике психических заболеваний существует несколько отличающихся теорий о происхождении и симптоматике шизофрении.
Неопределенность знаний приводит к тому, что правила влияния даже в простых случаях не всегда дают корректные результаты. Располагая неполным знанием, мы не можем уверенно предсказать, какой эффект даст то или иное действие. Например, терапия, использующая новые препараты, довольно часто дает совершенно неожиданные результаты. И, наконец, даже когда мы располагаем достаточно полной теорией предметной области, эксперт может посчитать, что эффективнее использовать не точные, а эвристические методы. Так, методика устранения неисправности в электронном блоке путем замены подозрительных узлов оказывается значительно более эффективной, чем скрупулезный анализ цепей в поиске детали, вышедшей из строя.
Но помимо неточных знаний, неопределенность может быть внесена и неточными или ненадежными данными о конкретной ситуации. Любой сенсор имеет ограниченную разрешающую способность и отнюдь не стопроцентную надежность. При составлении отчетов могут быть допущены ошибки или в них могут попасть недостоверные сведения. На практике далеко не всегда можно получить полные ответы на поставленные вопросы и хотя можно воспользоваться различного рода дополнительной информацией о пациенте, например с помощью дорогостоящих процедур или хирургическим путем, такие методики используются крайне редко из-за высокой стоимости и рискованности. Помимо всего прочего, существует еще и фактор времени.
Не всегда есть возможность быстро получить необходимые данные, когда ситуация требует принятия срочного решения. Если работа ядерного реактора вызывает подозрение, вряд ли кто-нибудь будет ждать окончания всего комплекса проверок, прежде чем принимать решение о его остановке.
Суммируя все сказанное, отметим, что эксперты пользуются неточными методами по двум главным причинам:
точных методов не существует;
точные методы существуют, но не могут быть применены на практике из-за отсутствия необходимого объема данных или невозможности их накопления по соображениям стоимости, риска или из-за отсутствия времени на сбор необходимой информации.
Большинство исследователей, занимающихся проблемами искусственного интеллек: та, давно пришли к единому мнению, что неточные методы играют важную роль в разработке экспертных систем, но много споров вызывает вопрос, какие именно методы должны использоваться. До последнего времени многие соглашались с утверждениями Мак-Карти и Хейеса, чт.о теория вероятности не является адекватным инструментом для решения задач представления неопределенности знаний и данных [McCarthy and Hayes, 1969]. Выдвигались следующие аргументы в пользу такого мнения:
теория вероятности не дает ответа на вопрос, как комбинировать вероятности с количественными данными (см. об этом в главе 8);
назначение вероятности определенным событиям требует информации, которой мы просто не располагаем.
Другие исследователи прибавляли к этим аргументам свои:
непонятно, как количественно оценивать такие часто встречающиеся на практике понятия, как "в большинстве случаев", "в редких случаях", или такие приблизительные оценки, как "старый" или "высокий";
применение теории вероятности требует "слишком много чисел", что вынуждает инженеров давать точные оценки тем параметрам, которые они не могут оценить;
обновление вероятностных оценок обходится очень дорого, поскольку требует большого объема вычислений.
Все эти соображения породили новый формальный аппарат для работы с неопределенностями, который получил название нечеткая логика (fuzzy logic) или теория функций доверия (belieffunctions). Этот аппарат широко используется при решении задач искусственного интеллекта и особенно при построении экспертных систем.Нечеткая логика будет рассмотрена ниже в этой главе, а о теории функций доверия (ее также называют теорией признаков Демпстера— Шафера) мы поговорим в главе 21. Однако в последние годы адвокаты теории вероятностей предприняли довольно эффективную контратаку, а потому мы также представим читателям основные концепции этой теории и ее главных конкурентов, а обзор дальнейшего развития работ в этом направлении отложим до следующей главы.
Экспертные системы и теория вероятностей
В этом разделе будут рассмотрены те аспекты теории вероятностей, которые имеют отношение к представлению неопределенностей. Мы начнем с понятия условной вероятности и остановимся на тех причинах, по которым вероятностный подход критикуется большинством исследователей, занимающихся экспертными системами. Затем мы вернемся к коэффициентам уверенности, которые обсуждались в главе 3 в связи с системой MYCIN, рассмотрим их подробнее и сравним результаты, которые получаются при использовании этого аппарата и аппарата теории вероятностей.
Коэффициенты уверенности
Теперь мы вернемся к коэффициентам уверенности, о которых уже шла речь в главе 3, когда мы рассматривали принципы работы системы MYCIN.
В идеальном мире можно вычислить вероятность P(di| E), где di — i-я диагностическая категория, а £ представляет все необходимые дополнительные свидетельства или фундаментальные знания, используя только вероятности P(di | Sj), где Sj является j-м клиническим наблюдением (симптомом). Мы уже имели возможность убедиться в том, что правило Байеса позволяет выполнить такие вычисления только в том случае, если, во-первых, доступны все значения P(sj | di), и, во-вторых, правдоподобно предположение о взаимной независимости симптомов.
В системе MYCIN применен альтернативный подход на основе правил влияния, которые следующим образом связывают имеющиеся данные (свидетельства) с гипотезой решения:
ЕСЛИ
пациент имеет показания и симптомы s1 ^ ...^ sk и имеют место определенные фоновые условия t1 ^ ... ^ fm ,
ТО
можно с уверенностью т заключить, что пациент страдает заболеванием di.
Коэффициент-уверенности t принимает значения в диапазоне [-1,+ 1]. Если т = +1, то это означает, что при соблюдении всех оговоренных условий составитель правила абсолютно уверен в правильности заключения di, а если т = -1, то значит, что при соблюдении всех оговоренных условий существует абсолютная уверенность в ошибочности этого заключения. Отличные от +1 положительные значения коэффициента указывают на степень уверенности в правильности заключения di, а отрицательные значения — на степень уверенности в его ошибочности.
Основная идея состоит в том, чтобы с помощью порождающих правил такого вида попытаться заменить вычисление P(di | s1 ^ ... ^ sk) приближенной оценкой и таким образом сымитировать процесс принятия решения экспертом-человеком. Как было показано в главе 3, результаты применения правил такого вида связываются с коэффициентом уверенности окончательного заключения с помощью CF(a) — коэффициент уверенности в достоверности значения параметра а, а дополнительные условия t1 ^ ... ^ tm представляют фоновые знания, которые ограничивают применение конкретного правила.
Чаще всего оказывается, что эти условия могут быть интерпретированы значениями "истина" или "ложь", т.е. соответствующие коэффициенты принимают значение +1 или -1. Таким образом, отличные от единицы значения коэффициентов характеризуют только симптомы s1, ... , sk. Роль фоновых знаний состоит в том, чтобы разрешить или запретить применение правила в данном конкретном случае. Пусть, например, имеется диагностическое правило, связывающее появление болей в брюшной полости с возможной беременностью. Применение этого правила блокируется фоновым знанием, что оно справедливо только по отношению к пациентам-женщинам.
Бучанан и Шортлифф утверждают, что, строго говоря, применение правила Байеса в любом случае не позволяет получить точные значения, поскольку используемые условные вероятности субъективны [Buchanan and Shortliffe, 1984, Chapter 11]. Как мы уже видели, это основной аргумент против применения вероятностного подхода. Однако такая аргументация предполагает объективистскую интерпретацию понятия вероятности, т.е. предполагается, что "правильные" значения все же существуют, но мы не можем их получить, а раз так, то и правило Байеса нельзя использовать. Этот аргумент имеет явно схоластический оттенок, поскольку любая экспертиза, проводимая инженером по знаниям, совершенно очевидно сводится к представлению тех знаний о предметной области, которыми обладает человек-эксперт (эти знания, конечно же, являются субъективными), а не к воссозданию абсолютно адекватной модели мира. С точки зрения теории представляется, что целесообразнее использовать математически корректный формализм к неточным данным, чем формализм, который математически некорректен, к тем же неточным данным.
Перл обратил внимание на важное практическое достоинство подхода, основанного на правилах [Pearl, 1988, р.5]. Вычисление коэффициентов уверенности заключения имеет явно выраженный модульный характер, поскольку не нужно принимать во внимание никакой иной информации, кроме той, что имеется в данном правиле.
При этом не имеет никакого значения, как именно получены коэффициенты уверенности, характеризующие исходные данные.
При построении экспертных систем часто используется эта особенность. Полагается, что для всех правил, имеющих дело с определенным параметром, предпосылки каждого правила логически независимы. Анализируя систему MYCIN, Шортлифф посоветовал сгруппировать все зависимые признаки в единое правило, а не распределять их по множеству правил (см., например, [Buchanan and Shortliffe, 1984, p. 229]).
Пусть, например, существует зависимость между признаками Е1 и E2- Шортлифф рекомендует сгруппировать их в единое правило если E1 и Е2, то приходим к заключению Н с уверенностью т, а не распределять по двум правилам если E1, то приходим к заключению Н с уверенностью t, если Е2, то приходим к заключению Н с уверенностью t.
В основе этой рекомендации лежит одно из следствий теории вероятностей, гласящее, что Р(Н | E1, Е2) не может быть простой функцией от Р(Н | Е1) и Р(Н | Е2).
Выражения для условной вероятности не могут в этом смысле рассматриваться как модульные. Выражение
P(B | A) = t
не позволяет заключить, что Р(В) = t при наличии А, если только А не является единственным известным признаком. Если кроме А мы располагаем еще и знанием Е, то нужно сначала вычислить Р(В | А, Е), а уже потом можно будет что-нибудь сказать и о значении Р(В). Такая чувствительность к контексту может стать основой очень мощного механизма логического вывода, но, как уже не раз подчеркивалось, за это придется платить существенным повышением сложности вычислений.
Коэффициенты уверенности и условные вероятности
9.2.3. Коэффициенты уверенности и условные вероятности
Адаме показал, что если используется простая вероятностная модель на основе правила Байеса, то в системе MYCIN коэффициенты уверенности гипотез не соответствуют вероятностям гипотез при заданных признаках [Adams, 1976]. На первый взгляд, если коэффициенты уверенности используются только для упорядочения альтернативных гипотез, это не очень страшно. Но Адаме также показал, что возможна ситуация, когда при использовании коэффициентов уверенности две гипотезы будут ранжированы в обратном порядке по отношению к соответствующим вероятностям. Рассмотрим этот вопрос подробнее.
Обозначим через Р(h) субъективное, т.е. составленное на основе заключения эксперта, значение вероятности того, что гипотеза h справедлива, т.е. значение Р(Н) отражает степень уверенности эксперта в справедливости гипотезы h. Усложним положение дел и добавим новый признак е в пользу этой гипотезы, такой что P(h | е) > Р(h). Степень доверия эксперта к справедливости гипотезы увеличится, и это увеличение выразится отношением
MB(h,e)= [P(h|e)-P(h)]/[1-P(h)]
где MB означает относительную меру доверия.
Если же признак е свидетельствует против гипотезы h, т.е. P(h | е) < P(h), то увеличится мера недоверия эксперта к справедливости этой гипотезы. Меру недоверия MD можно выразить следующим отношением:
MD(h, e) =[P(h)-P(h|e) ] / P(h)]
Адаме обратил внимание на то, что уровни доверия к одной и той же гипотезе с учетом разных дополнительных признаков не могут быть определены независимо. Если некоторый признак является абсолютным диагностическим индикатором конкретного заболевания, т.е. если все пациенты с симптомом s1 страдают заболеванием dj, то никакие другие признаки уже не могут изменить диагноз, т.е. уровень доверия к выдвинутой гипотезе. Другими словами, если существует пара признаков s1 и s2 и
P(di|s1)=P(di|S1^S2)=1,
то
P(di|s2)= P(dl).
Адаме также критически отнесся к объединению (конъюнкции) гипотез. Модель, положенная в основу MYCIN, предполагает, что уровень доверия к сочетанию гипотез d1 ^ d2 должен соответствовать наименьшему из уровней доверия отдельных гипотез, а уровень недоверия — наибольшему из уровней недоверия отдельных гипотез.
Предположим, что гипотезы d1 и d2 не только не независимы, но и взаимно исключают друг друга. Тогда P(d1 ^ d2 | е) = 0 при наличии любого признака е и независимо от степени доверия или недоверия к d1 или d2
Бучанан и Шортлифф определили коэффициент уверенности как некий артефакт, который позволяет численно оценить комбинацию уровней доверия или недоверия к гипотезам [Buchanan and Shortliffe, 1984, p. 249]. Он представляет собой разницу между мерой доверия и недоверия:
CF(h, еа ^ ef ) = MB(h, ef) - MD(h, ea),
где ef— признак, свидетельствующий в пользу гипотезы h, a ea — признак, свидетельствующий против гипотезы h. Однако полученное таким образом значение отнюдь не эквивалентно условной вероятности существования гипотезы h при условии еа ^ ef, которое следует из правила Байеса:
P(h|ea^ef)=[P(ea^ef | h)P(h)]/[P(ea^ef )]
Таким образом, хотя степень доверия, связанная с определенным правилом, и может быть соотнесена с субъективной оценкой вероятности, коэффициент уверенности является комбинированной оценкой. Его основное назначение состоит в следующем:
управлять ходом выполнения программы при формировании суждений;
управлять процессом поиска цели в пространстве состояний: если коэффициент уверенности гипотезы оказывается в диапазоне [+0.2, -0.2], то поиск блокируется;
ранжировать набор гипотез после обработки всех признаков.
Адаме, однако, показал, что ранжирование гипотез на основе коэффициентов уверенности может дать результат, противоположный тому, который будет получен при использовании вероятностных методов. Он продемонстрировал это на следующем примере.
Положим, что d1u d2 — это две гипотезы, а е — признак, свидетельствующий как в пользу одной гипотезы, так и в пользу другой. Пусть между априорными вероятностями существует отношение P(d1) > P(d2) и P(d\ \ е) > P(d2 | е). Другими словами, субъективная вероятность справедливости гипотезы d\ больше, чем гипотезы d2, причем это соотношение сохраняется и после того, как во внимание принимается дополнительный признак.
Адаме показал, что при этих условиях возможно обратное соотношение CF(d1, е) < CF(d2, е) между коэффициентами уверенности гипотез.
Предположим, что вероятности имеют следующие значения:
P(d1) = 0.8,
P(d2) = 0.2,
P(d1|e) = 0.9,
P(d2| e) = 0.8.
Тогда повышение доверия к d1 будет равно (0.9 - 0.8) / 0.2 = 0.5, а повышение доверия к
d2 — (0.8 - 0.2) / 0.8 = 0.75.
Отсюда следует, что CF(d1| e) < CF(d2, е), несмотря на то, что и P(d1 | e) > P(d2| е).
Адаме назвал это явление "нежелательным свойством" коэффициентов доверия. Избежать такой ситуации можно, если все априорные вероятности будут равны. Несложно показать, что эффект в приведенном выше примере явился следствием того, что признак е больше свидетельствовал в пользу гипотезы d2, чем в пользу d1, именно из-за более высокой априорной вероятности последней. Однако приравнивание априорных вероятностей явно не согласуется со стилем мышления тех, кто ставит диагноз, поскольку существует достаточно большое отличие в частоте сочетаний разных болезней с одинаковыми симптомами, следовательно, эксперты будут присваивать им совершенно разные значения субъективных вероятностей.
Последовательное применение правил в системе MYCIN также связано с существованием определенных теоретических проблем. Используемая при этом функция комбинирования основана на предположении, что если признак е влияет на некоторую промежуточную гипотезу h с вероятностью P(h | е), а гипотеза h входит в окончательный диагноз d с вероятностью P(d | h), то
P(d|e) = P(d|h)P(h|e).
Таким образом, создается впечатление, что транзитивное отношение в последовательности правил вывода суждений справедливо на первом шаге, но не справедливо в общем случае. Для того чтобы существовала связь между правилами, популяции, связанные с этими категориями, должны быть вложены примерно так, как на рис. 9.1.
Рис. 9.1. Популяции, позволяющие использовать P(d | е; = P(d| h)P(h| z)
Адаме пришел к выводу, что успех практического применения системы MYCIN и других подобных систем объясняется тем, что в них используются довольно короткие последовательности комбинирования правил, а рассматриваемые гипотезы довольно просты.
Другое критическое замечание относительно MYCIN было высказано Горвицем и Гекерманом и касается использования коэффициентов уверенности в качестве меры изменения доверия, в то время как в действительности они устанавливаются экспертами в качестве степени абсолютного доверия [Horvitz and Heckerman, 1986]. Связывая коэффициенты доверия с правилами, эксперт отвечает на вопрос: "Насколько вы уверены в правдоподобности того или иного заключения?" При применении в MYCIN функций комбинирования дополнительных признаков эти коэффициенты становятся мерой обновления степени доверия, что приводит к несовместимости этих значений с теоремой Байеса.
Нечеткая логика
Ту роль, которую в классической теории множеств играет двузначная булева логика, в теории нечетких множеств играет многозначная нечеткая логика, в которой предположения о принадлежности объекта множеству, например FAST-CAR(Porche-944), могут принимать действительные значения в интервале от 0 до 1. Возникает вопрос, а как, используя концепцию неопределенности, вычислить значение истинности сложного выражения, такого как
¬FAST¬CAR(Chevy-Nova).
По аналогии с теорией вероятности, если F представляет собой нечеткий предикат, операция отрицания реализуется по формуле
¬F(X)=1-F(X).
Но аналоги операций конъюнкции и дизъюнкции в нечеткой логике не имеют никакой связи с теорией вероятностей. Рассмотрим следующее выражение:
"Porche 944 является быстрым (fast), представительским (pretentious) автомобилем". В классической логике предположение
FAST-CAR(Porche-944) ^PRETENTIOUS-CAR(Porche-944)
является истинным в том и только в том случае, если истинны оба члена конъюнкции. В нечеткой логики существует соглашение: если F и G являются нечеткими предикатами, то
Таким образом, если
FAST-CAR(Porche-944) = 0.9
PRETENTIOUS-CAR(Porche-944) = 0.7,
то
FAST-CAR(Porche-944) ^ PRETENTIOUS-CAR(Porche-944) = 0.7.
А теперь рассмотрим выражение
FAST-CAR(Porche-944) ^ ¬FAST-CAR(Porche-944).
Вероятность истинности этого утверждения равна 0, поскольку
P(FAST-CAR(Porche-944) | ¬FAST-CAR(Porche-944)) = 0,
но в нечеткой логике значение этого выражения будет равно 0.1 . Какой смысл имеет это значение. Его можно считать показателем принадлежности автомобиля к нечеткому множеству среднескоростных автомобилей, которые в чем-то близки к быстрым, а в чем-то — к медленным.
Смысл выражения FAST-CAR(Porche-944) = 0.9 заключается в том, что мы только на 90% уверены в принадлежности этого автомобиля к быстрым именно из-за неопределенности самого понятия "быстрый автомобиль". Вполне резонно предположить, что существует некоторая уверенность в том, что Porche-944 не принадлежит к быстрым, например он медленнее автомобиля, принимающего участие в гонках "Формула-1".
Нечеткие множества
То знание, которое использует эксперт при оценке признаков или симптомов, обычно базируется скорее на отношениях между классами данных и классами гипотез, чем на отношениях между отдельными данными и конкретными гипотезами. Большинство методик .решения проблем в той или иной форме включает классификацию данных (сигналов, симптомов и т.п.), которые рассматриваются как конкретные представители некоторых более общих категорий. Редко когда эти более общие категории могут быть четко очерчены. Конкретный объект может обладать частью характерных признаков определенной категории, а частью не обладать, принадлежность конкретного объекта к определенному классу может быть размыта. Предложенная Заде [Zadeh, 1965] теория нечетких множеств (fuzzy set theory) представляет собой формализм, предназначенный для формирования суждений о таких категориях и принадлежащих к ним объектах. Эта теория лежит в основе нечеткой логики (fuzzy logic) [Zadeh, 1975] и теории возможностей (possibility theory) [Zadeh, 1978].
Классическая теория множеств базируется на двузначной логике. Выражения в форме а & А, где а представляет индивидуальный объект, а А — множество подобных объектов, могут принимать только значение "истина" либо "ложь". После появления понятия "нечеткое множество" прежние классические множества иногда стали называть жесткими. Жесткость классической теории множеств стала источником ряда проблем при попытке применить ее к нечетко определенным категориям.
Рассмотрим категорию, определенную словом "быстрый" (fast). Если применить это определение к автомобилям, то какой автомобиль можно считать быстрым? В классической теории мы можем определить множество А "быстрых автомобилей" либо перечислением (составив список всех членов множества), либо введя в рассмотрение некоторую характеристическую функцию f такую, что для любого объекта X
f(X) = истина тогда и только тогда, когда Х принадлежит А.
Например, эта функция может отбирать только те автомобили, которые имеют скорость более 150 миль в час:
Неопределенное состояние проблемы неопределенности
Одно из главных достоинств формализма нечеткой логики в применении к экспертным системам состоит в возможности комбинирования его логических операторов. Ранее мы уже отмечали, что для правила MYCIN
ЕСЛИ
пациент имеет показания и симптомы s1 ^ ... ^ sk и
имеют место определенные фоновые условия t1 ^ ... ^ tm ,
ТО можно с уверенностью т заключить, что пациент страдает заболеванием di
оценка набора симптомов s1 ^ ... ^ sk, в соответствии с аксиомами теории вероятностей, включает вычисление произведений вида
P(s1 | s2 ^.. ,^ sk )P(s2 | s3 ^.. .^ sk )... P(sk)
Такая операция в худшем случае требует вычисления k-1 оценки вероятностей свыше тех, что необходимы для si.
Было также показано, что в MYCIN конъюнкция интерпретируется как оператор нечеткой логики, — при этом вычисляется min (s1^ ...^ sk). Это может иногда привести к результатам, полностью противоположным тем, которые следуют из теории вероятностей. Прк сравнении результатов, полученных с помощью различных методов обработки неопределенности в практических системах, были найдены и другие примеры ошибочных выводов, Это сравнение показало, что методы, основанные на нечеткой логике, менее надежны, чем те, которые используют Байесовский подход (см., например, [Wise and Henrion, 1986]).
С другой стороны, нелишне отметить, что человеку также не свойственно строить суждения на основе Байесовского подхода. Исследования Канемана и Тверского показали, что люди склонны не принимать во внимание прежний опыт и отдавать предпочтение более свежей информации [Kahneman and Tversky, 1972]. Некоторые исследователи полагают, что людям свойственно переоценивать свою компетентность (см., например, статьи в сборнике [Kahneman et al, 1982]), причем большинство имеют слабое представление о теории оценок [Tversky and Kahneman, 1974].
Частично привлекательность нечеткой логики для проектировщиков экспертных систем состоит в ее близости к естественному языку. Таким терминам, как "быстрый", "немного", "правдоподобно", чаще всего дается интерпретация на основе повседневного опыта и интуиции. Это упрощает процесс инженерии знаний, поскольку подобные суждения человека-эксперта можно непосредственно преобразовать в выражения нечеткой логики.
Мы еще вернемся к нечеткой логике в главе 21. Здесь же были изложены только основные идеи, чтобы читатель мог получить первое представление о концепции неопределенности знаний и данных и связанных с этим проблемах. Но даже из этого краткого изложения ясно, что предстоит еще очень много сделать для того, чтобы иметь полное понятие об адекватном представлении неопределенности в технических системах.
Представление неопределенности знаний и данных
9.1. Источники неопределенности
9.2. Экспертные системы и теория вероятностей
9.3. Сомнительность и возможность
9.4. Неопределенное состояние проблемы неопределенности Рекомендуемая литература
Упражнения
Во многих реальных приложениях приходится сталкиваться с ситуацией, когда автоматический решатель задач имеет дело с неточной информацией. В этой главе мы рассмотрим основные идеи, касающиеся количественной оценки неопределенности и методов формирования нечетких суждений. В главах 11-15 будет продемонстрировано, как такие методы используются на практике. В настоящей главе речь пойдет в основном о теоретических аспектах представления неопределенности и о том, почему в исследованиях по искусственному интеллекту такое большое внимание уделяется этим проблемам. В главе 21 мы вновь вернемся к проблеме неопределенности и рассмотрим ее более глубоко, но для большинства читателей вполне достаточно будет и тех сведений, которые представлены в данной главе.
Подробное изложение методики применения коэффициентов уверенности в системе MYCIN читатель найдет в части 4 книги Бучанана и Шортлиффа [Buchanan and Shartliffe, 1984]. В этой же книге воспроизведена критическая статься Адамса. В сборнике [Mamdani and Games, 1981] собраны статьи зачинателей теории нечеткой логики. Книга Санфорда [Sanford, 1987] содержит популярное изложение исследований в области психологических аспектов теории возможностей.
Наиболее свежие работы в области нечеткой логики опубликованы в сборниках [Baldwin, 1996], [Dubois et al, 1996], [Jamshidi et al., 1997]. В книге [Walker and Nguyen, 1996] представлен вводный курс нечеткой логики, а в книге [Yager and Filev, 1994] описано применение идей нечеткой логики в моделировании и управлении. Книга [McNeill and Freiberger, 1993] предназначена для читателей-неспециалистов и содержит описание истории нечетких суждений, сопровождаемое множеством анекдотов и исторических фактов.
Сомнительность и возможность
Помимо использования коэффициентов уверенности, в литературе описаны и иные подходы, альтернативные вероятностному. В частности, много внимания уделяется нечеткой логике (fuzzy logic) и теории функций доверия (belieffunctions). О функциях доверия мы поговорим в главе 21, а в данном разделе читатель познакомится с основными аспектами нечеткой логики. Будет показано, почему подход, основанный на идеях нечеткой логики, в последнее время все шире используется при создании экспертных систем.
Теория возможности
Нечеткая логика имеет дело с ситуациями, когда и сформулированный-вопрос, и знания, которыми мы располагаем, содержат нечетко очерченные понятия. Однако нечеткость формулировки понятий является не единственным источником неопределенности. Иногда мы просто не уверены в самих фактах. Если утверждается: "Возможно, что Джон сейчас в Париже", то говорить о нечеткости понятий Джон и Париж не приходится. Неопределенность заложена в самом факте, действительно ли Джон находится в Париже.
Теория возможностей является одним из направлений в нечеткой логике, в котором рассматриваются точно сформулированные вопросы, базирующиеся на неточных знаниях. В этом разделе вы познакомитесь только с основными идеями этой теории. Лучше всего это сделать на примере.
Предположим, что в ящике находится 1 0 шаров, но известно, что только несколько из них красных. Какова вероятность того, что на удачу из ящика будет вынут красный шар?
Просто вычислить искомое значение, основываясь на знаниях, что только несколько шаров красные (red), нельзя. Тем не менее для каждого значения X из P(RED) в диапазоне [0,1] можно следующим образом вычислить возможность, что P(RED) = Х.
Во-первых, определим "несколько" (several) как нечеткое множество, например, так:
fSEVERAL = {(3, 0.2), (4, 0.6), (5, 1.0), (6, 1.0), (7, 0.6), (8, 0.3)} .
В этом определении выражение (3, 0.2) е fSEVERAL означает, что 3 из 10 вряд ли можно признать как "несколько", а выражения (5, 1 .0) е fSEVERAL и (6, 1 .0) е fSEVERAL означают, что значения 5 и 6 из 10 идеально согласуются с понятием "несколько". Обратите внимание на то, что в определение нечеткого множества не входят значения 1 и 10, поскольку интуитивно ясно, что "несколько" означает "больше одного" и "не все". Нечеткое множество, определенное на множестве чисел, называется нечеткими числами (fuzzy numbers). По тому же принципу, что и множество fSEVERAL, можно определить нечеткие множествами/для понятия "мало" fMOST для понятия "почти".
Теперь распределение возможностей для P(RED) представляется формулой
fP(RED) = SEVERAL / 10,
которая после подстановки дает
{(0.3, 0.2), (0.4, 0.6), (0.5, 1.0), (0.6, 1.0), (0.7, 0.6), (0.8, 0.3)}.
Выражение (0.3, 0.2) ~ fP(RED) означает, что шанс на то, что P(RED) = 0.3, равен 20%. Можно рассматривать fP(RED) как нечеткую вероятность (fuzzy probability).
Полагая, что почти любое понятие может быть областью определения такой функции, естественно ввести в обиход и понятие "нечеткое значение правдоподобия". Мы часто оцениваем некоторое утверждение как "очень правдоподобное" или "частично правдоподобное". Таким образом, можно представить себе нечеткое множество
ftrue-: [0 , 1]-> [0, 1],
где и область определения, и область значений функции ftrue являются возможными значениями правдоподобия в нечеткой логике. Следовательно, можно получить
TRUE(FASR-CAR(Porsche-944)) = 1
даже при FASR-CAR(Porsche-944) = 0.9, поскольку (0.9, 1.0)~ftrue Это означает, что любое предположение относительно значения 0.9 рассматривается как "достаточно правдоподобное". Таким образом, можно с уверенностью сказать, что Porsche-944 является быстрым автомобилем, несмотря на то, что на рынке есть и более скоростные.
Какова вероятность того, что из
1. Какова вероятность того, что из полной колоды будет вытянута одна из старших карт (король, дама или валет)?
2. Какова вероятность того, что в каждом из двух последовательных бросаний игральной кости выпадет число больше трех?
3. Предположим, что вероятность отказа одного из двигателей трехмоторного самолета равна 0.01. Какова вероятность того, что откажут все три двигателя, если считать, что работоспособность одного двигателя не зависит от состояния двух других?
4. Какова вероятность того, что в примере упр. 3 откажут все три двигателя, если отказаться от предположения о независимости состояния двигателей, а использовать приведенные ниже значения условных вероятностей?
Р(отказ_двиг_1 | отказ_двиг_2 v отказ _двиг_3) =0.4
Р(отказ_двиг_2 | отказ_двиг_1 v отказ_двиг_3) = 0.3
Р(отказ_двиг_3 | отказ_двиг_1 v отказ_двиг_2) = 0.2
Р(отказ_двиг_1 отказ_двиг_2 v отказ_двиг_3) = 0.9
Р(отказ_двиг_2 | отказ_двиг_1 v отказ_двиг_3) = 0.8
Р(отказ_двиг_3 | отказ_двиг_1 v отказ_двиг_2) = 0.7
5. Положим, что Р(ртказ_трех_двиг | диверсия) = 0.9, а вероятность отказа любого отдельного двигателя, как и ранее, равна 0.01. Используя условные вероятности, представленные в упр. 4, определите, какова вероятность того, что была совершена диверсия, если известно, что отказали все три двигателя.
6. Поясните, в чем состоит отличие между частотной и субъективистской интерпретацией вероятности.
7. Почему во многих экспертных системах для вычисления степени уверенности в сделанном заключении не используется правило Байеса?
8. Какие проблемы могут появиться при использовании следующей пары правил системы MYCIN? Какие особенности структуры управления в MYCIN усугубляют ситуацию?
если Е1, то Н c уверенностью +0.5, если Е1 и £2, то Н с уверенностью -0.5.
Как следует скорректировать данные правила, чтобы избежать появления этих проблем?
9. Предположим, что понятие "немного" определено как нечеткое множество:
fНЕМНОГО = {(3, 0.8), (4, 0.7), (5, 0.6), (6, 0.5), (7, 0.4), (8, 0.3)}.
В ящике находится 15 шаров и известно, что немногие из них синего цвета. Какова вероятность того, что наудачу из ящика будет вынут именно синий шар?
10. Предположим, что понятие "необычная оценка из десяти" определено как нечеткое множество:
fНЕОБЫЧНО = {(0, 1.0), (1, 0.9), (2, 0.7), (3, 0.5), (4, 0.3), (5, 0.1),
(6, 0.1), (7, 0.3), (8, 0.5), (9, 0.9), (10, 0.9)},
а понятие "высокая оценка из десяти" определено как нечеткое множество
f ВЫСОКАЯ= {(0, 0), (1, 0), (2, 0), (3, 0.1), (4, 0.2), (5, 0.3),
(6, 0.4), (7, 0.6), (8, 0.7), (9, 0.8), (10, 1.0)}.
Постройте составную функцию "необыкновенно высокая оценка из десяти".
Условная вероятность
Условная вероятность события d при данном s — это вероятность того, что событие d наступит при условии, что наступило событие s. Например, вероятность того, что пациент действительно страдает заболеванием d, если у него (или у нее) обнаружен только симптом s.
В традиционной теории вероятностей для вычисления условной вероятности события d при данном s используется следующая формула:
P(d|s)=(d^ s)/P(S) (9.1)
Как видно, условная вероятность определяется в терминах совместимости событий. Она представляет собой отношение вероятности совпадения событий d и s к вероятности появления события s. Из формулы (9.1) следует, что
P(d^s)=P(d|s)P(d).
Если разделить обе части на P(s) и подставить в правую часть (9.1), то получим правило Байеса в простейшем виде:
P(d|s)=(s|d)P(d)/P(S) (9.2)
Это правило, которое иногда называют инверсной формулой для условной вероятности, позволяет определить вероятность P(d | s) появления события d при условии, что произошло событие s через известную условную вероятность P(s | d). В полученном выражении P(d) — априорная вероятность наступления события d, a P(d | s) — апостериорная вероятность, т.е. вероятность того, что событие d произойдет, если известно, что событие s свершилось.
Для систем, основанных на знаниях, формула (9.2) гораздо удобнее формулы (9.1), в чем вы сможете убедиться в дальнейшем.
Предположим, что у пациента имеется некоторый симптом заболевания, например боль в груди, и желательно знать, какова вероятность того, что этот симптом является следствием определенного заболевания, например инфаркта миокарда или перикардита (воспаление каверн в легких), или чего-нибудь менее серьезного, вроде несварения желудка. Для того чтобы вычислить вероятность Р(инфаркт миокарда боль в груди) по формуле (9.1), нужно знать (или оценить каким-либо способом), сколько человек в мире страдают таким заболеванием и сколько человек и больны инфарктом миокарда, и жалуются на боль в груди (т.е. имеют такой же симптом). Как правило, такая информация отсутствует, особенно последняя, которая нужна для вычисления вероятности Р (инфаркт миокарда л боль в груди). Таким образом, определение, данное формулой (9.1), в клинической практике не может быть использовано.
Отмеченная сложность получения нужной информации явилась причиной негативного отношения многих специалистов по искусственному интеллекту к вероятностному подходу вообще (см., например, [Charniak and McDermott, 1985, Chapter 8]). Это негативное отношение подкреплялось тем, что в большинстве классических работ по теории вероятностей понятие вероятности определялось как объективная частотность (частота появления при достаточно продолжительных независимых испытаниях).
Однако существует мнение, что эти базовые предположения небесспорны с точки зрения практических приложений (см., например, [Pearl, 1982] и [Cheeseman, 1985]). Сторонники такого подхода придерживаются субъективистской точки зрения на определение вероятности, который позволяет иметь дело с оценками совместного появления событий, а не с действительной частотой. Такой взгляд на вещи связывает вероятность смеси событий с субъективной верой в то, что событие действительно наступит.
Например, врач может не знать или не иметь возможности вычислить, какая часть пациентов, жалующихся на боль в груди, страдает инфарктом миокарда, но на основании собственного опыта он может оценить, у какой части его пациентов, страдающих этим заболеванием, встречался такой симптом. Следовательно, он может оценить значение вероятности Р(боль в груди | инфаркт миокарда). Субъективный взгляд на природу вероятности тесно связан с правилом Байеса по следующей причине. Предположим, мы располагаем достаточно достоверной оценкой вероятности P(s | а), где 5 означает симптом, a d— заболевание. Тогда по формуле (9.2) можно вычислить вероятность P(d\ s). Оценку вероятности P(d) можно взять из публикуемой медицинской статистики, а оценить значение P(s) врач может на основании собственных наблюдений.
Вычисление P(d | s) не вызывает затруднений, когда речь идет о единственном симптоме, т.е. имеется множество заболеваний D и множество симптомов S, причем для каждого члена из D нужно вычислить условную вероятность того, что у пациентов, страдающих этим заболеванием, наблюдался один определенный симптом из множества S. Тем не менее, если в множестве D имеется т членов, а в множестве S— п членов, потребуется вычислить тп + т + п оценок вероятностей.
Это отнюдь не простая работа, еcли в системе медицинской диагностики используется до 2000 видов заболеваний и огромное число самых разнообразных симптомов.
Но ситуация значительно усложняется, если мы попробуем включить в процесс составления диагноза не один симптом, а несколько.
В более общей форме правило Байеса имеет вид
P(d|s1^...^sk )= P(s1^...^sk|d)P(d)/P(s1^...^sk) (9.3)
и требует вычисления (mn)k + m + nk оценок вероятностей, что даже при небольшом значении А; очень много. Эти оценки вероятностей требуются нам по той причине, что в общем случае для вычисления P(s1 ^ ....^ sk) нужно предварительно вычислить произведения вида
P(s1 | s2 ^.. .^sk )P(s2 | s3 ^.. .^sK )... P(sk ) .
Однако, если предположить, что некоторые симптомы независимы друг от друга, объем вычислений существенно снижается. Независимость любой пары симптомов Si, и Sj означает, что
P(Si)=P(Sl|Sj),
из чего следует соотношение
P(Si^Sj)=P(Si)P(Sj).
Если все симптомы независимы, то объем вычислений будет таким же, как и в случае учета при диагнозе единственного симптома.
Но, даже если это и не так, в большинстве случаев можно предположить наличие условной независимости. Это означает, что пара симптомов s\ и Sj является независимой, поскольку в нашем распоряжении имеются какие-либо дополнительные свидетельства на этот счет или фундаментальные знания Е. Таким образом,
P(Si|Sj,E)=P(Si|E).
Например, если в моем автомобиле нет горючего и не работает освещение, я могу смело сказать, что эти симптомы независимы, поскольку моих познаний в устройстве автомобиля вполне достаточно, чтобы предположить, что между ними нет никакой причинной связи. Но если автомобиль не заводится и не работает освещение, то заявлять, что эти симптомы независимы, нельзя, поскольку они могут быть следствием одной и той же неисправности аккумуляторной батареи. Степень доверия к симптому "не работает освещение" только увеличится, если обнаружится, что к тому же и двигатель не заводится. Необходимость отслеживать такого рода связи в программе и соответственно корректировать степень доверия к симптомам значительно увеличивает объем вычислений в общем случае (см.
об этом в работе [Cooper, 1990]).
Таким образом, использование теории вероятности ставит перед нами следующие проблемы, которые лучше всего сформулировать в терминах задачи выбора:
либо априори предполагается, что все данные независимы, и использовать менее трудоемкие методы вычислений, за что придется платить снижением достоверности результатов;
либо нужно организовать отслеживание зависимости между используемыми данными, количественно оценить эту зависимость, реализовать оперативное обновление соответствующей нормативной информации, т.е. усложнить вычисления, но получить более достоверные результаты.
В главе 19 представлен обзор символических методов отслеживания зависимости между используемыми данными, а в главе 21 описаны некоторые численные методы моделирования зависимости между вероятностями.
В следующем разделе мы рассмотрим альтернативный подход, с помощью которого удается обойти указанные сложности при построении экспертных систем. Здесь же, а также в главе 21 будут проанализированы критические замечания, касающиеся этого подхода.
